
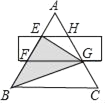
【题目】如图,等边△ABC被一个平行于BC的矩形所截,AB被截成三等份.若BC=a,则图中阴影部分的面积是_____.
【答案】![]()
【解析】
先由等边△ABC被一个平行于BC的矩形所截,AB被截成三等份,可得EH∥BC,那么△AEH∽△ABC,根据相似三角形面积比等于相似比的平方,得出S△AEH=![]() S△ABC,那么S梯形EBCH=
S△ABC,那么S梯形EBCH=![]() S△ABC.再证明FG是梯形EBCH的中位线,EH+BC=2FG.进而得到S△EBG=
S△ABC.再证明FG是梯形EBCH的中位线,EH+BC=2FG.进而得到S△EBG=![]() S梯形EBCH,从而求解即可.
S梯形EBCH,从而求解即可.
解:∵等边△ABC被一个平行于BC的矩形所截,AB被截成三等份,
∴AE=EF=FB=![]() AB=
AB=![]() BC=
BC=![]() a,EH∥BC,
a,EH∥BC,
∴△AEH∽△ABC,
∴ ,
,
∴S△AEH=![]() S△ABC,
S△ABC,
∴S梯形EBCH=S△ABC﹣S△AEH=![]() S△ABC.
S△ABC.
∵EH∥FG∥BC,EF=FB,
∴FG是梯形EBCH的中位线,
∴EH+BC=2FG.
设△EFG的边FG上的高为h,则△BFG的边FG上的高为h,梯形EBCH的高为2h,
∵S△EBG=S△EFG+S△ABFG
=![]() FGh+
FGh+![]() FGh
FGh
=FGh,
S梯形EBCH=![]() (EH+BC)2h
(EH+BC)2h
=![]() 2FG2h
2FG2h
=2FGh,
∴S△EBG=![]() S梯形EBCH=
S梯形EBCH=![]() ×
×![]()
![]() ×
×![]() a2=
a2=![]() a2.
a2.
故答案为![]() a2.
a2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将二次函数![]() 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与
的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,经过点
,经过点![]() 的一次函数
的一次函数![]() 的图象与
的图象与![]() 轴正半轴交于点
轴正半轴交于点![]() ,且与抛物线的另一个交点为
,且与抛物线的另一个交点为![]() ,
,![]() 的面积为5.
的面积为5.
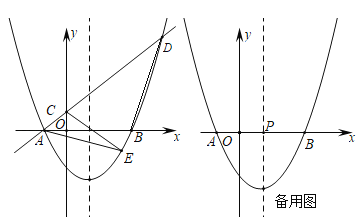
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点![]() 在一次函数的图象下方,求
在一次函数的图象下方,求![]() 面积的最大值,并求出此时点E的坐标;
面积的最大值,并求出此时点E的坐标;
(3)若点![]() 为
为![]() 轴上任意一点,在(2)的结论下,求
轴上任意一点,在(2)的结论下,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表:方程1、方程2、方程3、…是按一定规律排列的一列方程.
序号 | 方程 | 方程的解 | |
1 | x2+x﹣2﹣=0 | x1=﹣2 | x2=1 |
2 | x2+2x﹣8﹣=0 | x1=﹣4 | x2=2 |
3 | x2+3x﹣18=0 | x1= | x2= |
… | … | … | … |
(1)解方程3,并将它的解填在表中的空白处;
(2)请写出这列方程中第10个方程,并用求根公式求其解.
(3)根据表中的规律写出第n个方程和这个方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
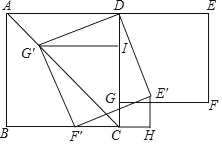
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网购已经成为一种时尚,某网络购物平台“双十一”全天交易额逐年增长,2016年交易额为500亿元,2018年交易额为720亿元。
(1)2016年至2018年“双十一”交易额的年平均增长率是多少?
(2)若保持原来的增长率,试计算2019年该平台“双十一”的交易额将达到多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
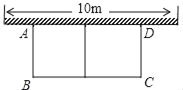
【题目】如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃,设花圃的一边AB为xm,面积为ym2.
(1)求y与x的函数关系式;
(2)如果要围成面积为48m2的花圃,AB的长是多少?
(3)能围成比48m2更大的花圃吗?如果能,请求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,且点
两点,且点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上.
轴的正半轴上.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角三角形纸片ABC中,∠ACB=90°,AC≤BC,如图,将纸片沿某条直线折叠,使点A落在直角边BC上,记落点为D,设折痕与AB、AC边分别交于点E、F.
(1)如果∠AFE=65°,求∠CDF的度数;
(2)若折叠后的△CDF与△BDE均为等腰三角形,那么纸片中∠B的度数是多少?写出你的计算过程,并画出符合条件的折叠后的图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌相机,原售价每台4000元,经连续两次降价后,现售价每台3240元,已知两次降价的百分率一样。
(1)求每次降价的百分率;
(2)如果按这个百分率再降价一次,求第三次降价后的售价?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com