
【题目】如表:方程1、方程2、方程3、…是按一定规律排列的一列方程.
序号 | 方程 | 方程的解 | |
1 | x2+x﹣2﹣=0 | x1=﹣2 | x2=1 |
2 | x2+2x﹣8﹣=0 | x1=﹣4 | x2=2 |
3 | x2+3x﹣18=0 | x1= | x2= |
… | … | … | … |
(1)解方程3,并将它的解填在表中的空白处;
(2)请写出这列方程中第10个方程,并用求根公式求其解.
(3)根据表中的规律写出第n个方程和这个方程的解.
【答案】(1)x1=﹣6,x2=3;(2)x1=10,x2=﹣20;(3)x1=﹣2n,x2=n.
【解析】
(1)可以利用因式分解法解方程,按照前两个方程的根的书写规律,第一个根是负数,第二个是正数,填表即可;
(2)仔细观察,发现规律,利用规律写出即可;
(3)根据根与系数的关系可知第n次方程的解是x1=-2n,x2=n,则方程就是x2+nx-2n2=0.
解:(1)∵x2+3x﹣18=0
即(x+6)(x﹣3)=0
∴x+6=0或x﹣3=0
∴x1=﹣6,x2=3;
故答案为:-6,3;
(2)方程规律:x2+1x﹣122=0,
x2+2x﹣222=0,
x2+3x﹣322=0,
即第10个方程为:x2+10x﹣1022=0,
所以第10个方程为:x2+10x﹣200=0,
解得x=![]() ,
,
∴x1=10,x2=﹣20;
(3)由(2)得:第n个方程为:x2+nx﹣2n2=0,
方程的两根为:x1=﹣2n,x2=n.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】长为![]() 的春游队伍,以
的春游队伍,以![]() 的速度向东行进,如图1和图2,当队伍排尾行进到位置
的速度向东行进,如图1和图2,当队伍排尾行进到位置![]() 时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为
时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为![]() ,当甲返回排尾后,他及队伍均停止行进.设排尾从位置
,当甲返回排尾后,他及队伍均停止行进.设排尾从位置![]() 开始行进的时间为
开始行进的时间为![]() ,排头与
,排头与![]() 的距离为
的距离为![]()
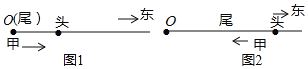
(1)当![]() 时,解答:
时,解答:
①求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围);
的取值范围);
②当甲赶到排头位置时,求![]() 的值;在甲从排头返回到排尾过程中,设甲与位置
的值;在甲从排头返回到排尾过程中,设甲与位置![]() 的距离为
的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
(2)设甲这次往返队伍的总时间为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围),并写出队伍在此过程中行进的路程.
的取值范围),并写出队伍在此过程中行进的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 ;
(2)当x 时,y随x的增大而减小;
(3)怎样移动抛物线![]() 就可以得到抛物线
就可以得到抛物线![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
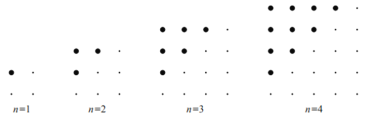
【题目】在下图中,每个正方形点阵由大点和小点组成:
(1)第7个正方形点阵中,大点和小点的总共的个数是________其中大点的个数是_________.
(2)第n个图形中,大点的个数是__________;(用含n的式子表示)
(3)是否存在某个图形,使得大点的个数是210个?若存在,请求出n的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
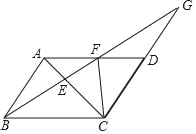
【题目】如图,AC是ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G.
(1)若∠ABF=∠ACF,求证:CE2=EFEG;
(2)若DG=DC,BE=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.
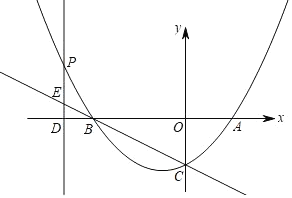
(1)求抛物线的函数表达式;
(2)若点P在第二象限内,且PE=![]() OD,求△PBE的面积.
OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,且
,且![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得
,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .
.
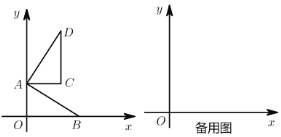
(1)点![]() 的坐标为______.
的坐标为______.
(2)解答下列问题:
①设![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ,并写出
,并写出![]() 的取值范围.
的取值范围.
②当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,这堵墙的长度为12米.计划建造车棚的面积为80平方米,已知现有的木板材料可使新建板墙的总长为26米.
(1)为了方便学生出行,学校决定在与墙平行的一面开一个2米宽的门,那么这个车棚的长和宽分别应为多少米?
(2)如图,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为54平方米,那么小路的宽为多少米?
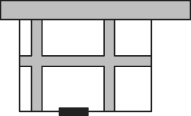
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com