
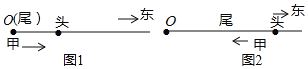
【题目】长为![]() 的春游队伍,以
的春游队伍,以![]() 的速度向东行进,如图1和图2,当队伍排尾行进到位置
的速度向东行进,如图1和图2,当队伍排尾行进到位置![]() 时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为
时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为![]() ,当甲返回排尾后,他及队伍均停止行进.设排尾从位置
,当甲返回排尾后,他及队伍均停止行进.设排尾从位置![]() 开始行进的时间为
开始行进的时间为![]() ,排头与
,排头与![]() 的距离为
的距离为![]()
(1)当![]() 时,解答:
时,解答:
①求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围);
的取值范围);
②当甲赶到排头位置时,求![]() 的值;在甲从排头返回到排尾过程中,设甲与位置
的值;在甲从排头返回到排尾过程中,设甲与位置![]() 的距离为
的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
(2)设甲这次往返队伍的总时间为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围),并写出队伍在此过程中行进的路程.
的取值范围),并写出队伍在此过程中行进的路程.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() 与
与![]() 的函数关系式为:
的函数关系式为:![]() ,此时队伍在此过程中行进的路程为
,此时队伍在此过程中行进的路程为![]() .
.
【解析】
(1)①排头与O的距离为S头(m).等于排头行走的路程+队伍的长300,而排头行进的时间也是t(s),速度是2m/s,可以求出S头与t的函数关系式;
②甲赶到排头位置的时间可以根据追及问题的数量关系得出,代入求S即可;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m)是在S的基础上减少甲返回的路程,而甲返回的时间=总时间t-甲从排尾赶到排头的时间,于是可以求S甲与t的函数关系式;
(2)甲这次往返队伍的总时间为T(s),是甲从排尾追到排头用的时间与从排头返回排尾用时的和,可以根据追及问题和相遇问题的数量关系得出结果;在甲这次往返队伍的过程中队伍行进的路程=队伍速度×返回时间.
(1)①排尾从位置O开始行进的时间为t(s),则排头也离开原排头t(s),∴S头=2t+300;
②甲从排尾赶到排头的时间为300÷(2v﹣v)=300÷v=300÷2=150 s,此时S头=2t+300=600 m,甲返回时间为:(t﹣150)s,∴S甲=S头﹣S甲回=2×150+300﹣4(t﹣150)=﹣4t+1200;
因此,S头与t的函数关系式为S头=2t+300,当甲赶到排头位置时,S的值为600m,在甲从排头返回到排尾过程中,S甲与t的函数关系式为S甲=﹣4t+1200.
(2)T=t追及+t返回![]() ,在甲这次往返队伍的过程中队伍行进的路程为:v
,在甲这次往返队伍的过程中队伍行进的路程为:v![]() 400;
400;
因此T与v的函数关系式为:T![]() ,此时队伍在此过程中行进的路程为400m.
,此时队伍在此过程中行进的路程为400m.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
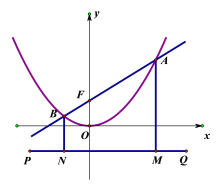
【题目】已知直线l:y=kx+4与抛物线y=![]() x2交于点A(x1,y1),B(x2,y2).
x2交于点A(x1,y1),B(x2,y2).
(1)求:![]() ;
;![]() 的值.
的值.
(2)过点(0,-4)作直线PQ∥x轴,且过点A、B分别作AM⊥PQ于点M,BN⊥PQ于点N,设直线l:y=kx+4交y轴于点F.求证:AF=AM=4+y1.
(3)证明:![]() +
+![]() 为定值,并求出该值.
为定值,并求出该值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=4![]() ,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为 ( )
,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为 ( )

A. 3![]() B. 2
B. 2![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于题目:“如图1,平面上,正方形内有一长为![]() 、宽为
、宽为![]() 的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数
的矩形,它可以在正方形的内部及边界通过移转(即平移或旋转)的方式,自由地从横放移转到竖放,求正方形边长的最小整数![]() .”甲、乙、丙作了自认为边长最小的正方形,先求出该边长
.”甲、乙、丙作了自认为边长最小的正方形,先求出该边长![]() ,再取最小整数
,再取最小整数![]() .
.
甲:如图2,思路是当![]() 为矩形对角线长时就可移转过去;结果取
为矩形对角线长时就可移转过去;结果取![]() .
.
乙:如图3,思路是当x为矩形外接圆直径长时就可移转过去;结果取n=14.
丙:如图4,思路是当![]() 为矩形的长与宽之和的
为矩形的长与宽之和的![]() 倍时就可移转过去;结果取
倍时就可移转过去;结果取![]() .
.
下列正确的是( )

A.甲的思路错,他的![]() 值对
值对
B.乙的思路和他的![]() 值都对
值都对
C.甲和丙的![]() 值都对
值都对
D.甲、乙的思路都错,而丙的思路对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图
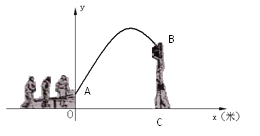
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,其部分图象如图所示,下列结论:①抛物线过点
,其部分图象如图所示,下列结论:①抛物线过点![]() ;②
;②![]() ;③
;③![]() ;④抛物线的顶点坐标为
;④抛物线的顶点坐标为![]() ;⑤当
;⑤当![]() 时,
时,![]() 随
随![]() 增大而增大.其中结论错误的是( )
增大而增大.其中结论错误的是( )
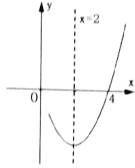
A.②③④B.②③⑤C.③⑤D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将二次函数![]() 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与
的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,经过点
,经过点![]() 的一次函数
的一次函数![]() 的图象与
的图象与![]() 轴正半轴交于点
轴正半轴交于点![]() ,且与抛物线的另一个交点为
,且与抛物线的另一个交点为![]() ,
,![]() 的面积为5.
的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点![]() 在一次函数的图象下方,求
在一次函数的图象下方,求![]() 面积的最大值,并求出此时点E的坐标;
面积的最大值,并求出此时点E的坐标;
(3)若点![]() 为
为![]() 轴上任意一点,在(2)的结论下,求
轴上任意一点,在(2)的结论下,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表:方程1、方程2、方程3、…是按一定规律排列的一列方程.
序号 | 方程 | 方程的解 | |
1 | x2+x﹣2﹣=0 | x1=﹣2 | x2=1 |
2 | x2+2x﹣8﹣=0 | x1=﹣4 | x2=2 |
3 | x2+3x﹣18=0 | x1= | x2= |
… | … | … | … |
(1)解方程3,并将它的解填在表中的空白处;
(2)请写出这列方程中第10个方程,并用求根公式求其解.
(3)根据表中的规律写出第n个方程和这个方程的解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com