
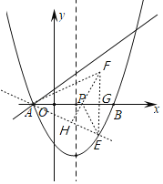
【题目】在平面直角坐标系中,将二次函数![]() 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与
的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,经过点
,经过点![]() 的一次函数
的一次函数![]() 的图象与
的图象与![]() 轴正半轴交于点
轴正半轴交于点![]() ,且与抛物线的另一个交点为
,且与抛物线的另一个交点为![]() ,
,![]() 的面积为5.
的面积为5.
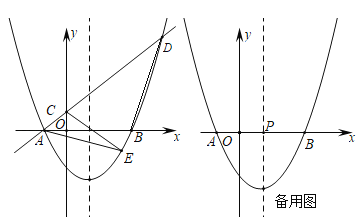
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点![]() 在一次函数的图象下方,求
在一次函数的图象下方,求![]() 面积的最大值,并求出此时点E的坐标;
面积的最大值,并求出此时点E的坐标;
(3)若点![]() 为
为![]() 轴上任意一点,在(2)的结论下,求
轴上任意一点,在(2)的结论下,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() 的面积最大值是
的面积最大值是![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;(3)
;(3)![]() 的最小值是3.
的最小值是3.
【解析】
(1)先写出平移后的抛物线解析式,再把点![]() 代入可求得
代入可求得![]() 的值,由
的值,由![]() 的面积为5可求出点
的面积为5可求出点![]() 的纵坐标,代入抛物线解析式可求出横坐标,由
的纵坐标,代入抛物线解析式可求出横坐标,由![]() 、
、![]() 的坐标可利用待定系数法求出一次函数解析式;
的坐标可利用待定系数法求出一次函数解析式;
(2)作![]() 轴交
轴交![]() 于
于![]() ,如图,利用三角形面积公式,由
,如图,利用三角形面积公式,由![]() 构建关于E点横坐标的二次函数,然后利用二次函数的性质即可解决问题;
构建关于E点横坐标的二次函数,然后利用二次函数的性质即可解决问题;
(3)作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,则
,则![]() ,利用锐角三角函数的定义可得出
,利用锐角三角函数的定义可得出![]() ,此时
,此时![]() 最小,求出最小值即可.
最小,求出最小值即可.
解:(1)将二次函数![]() 的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为
的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为![]() ,
,
∵![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() ,
,
代入抛物线的解析式得,![]() ,∴
,∴![]() ,
,
∴抛物线的解析式为![]() ,即
,即![]() .
.
令![]() ,解得
,解得![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() 的面积为5,∴
的面积为5,∴![]() ,∴
,∴![]() ,
,
代入抛物线解析式得,![]() ,解得
,解得![]() ,
,![]() ,∴
,∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
∴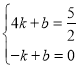 ,解得:
,解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,如图,设
,如图,设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() 的面积有最大值,最大值是
的面积有最大值,最大值是![]() ,此时
,此时![]() 点坐标为
点坐标为![]() .
.
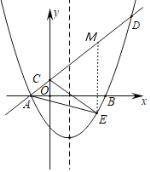
(3)作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴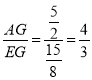 ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() 、
、![]() 关于
关于![]() 轴对称,∴
轴对称,∴![]() ,
,
∴![]() ,此时
,此时![]() 最小,
最小,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() 的最小值是3.
的最小值是3.


科目:初中数学 来源: 题型:
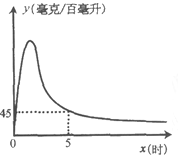
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间![]() (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数![]() 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当![]() =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
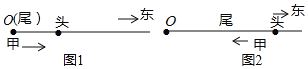
【题目】长为![]() 的春游队伍,以
的春游队伍,以![]() 的速度向东行进,如图1和图2,当队伍排尾行进到位置
的速度向东行进,如图1和图2,当队伍排尾行进到位置![]() 时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为
时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为![]() ,当甲返回排尾后,他及队伍均停止行进.设排尾从位置
,当甲返回排尾后,他及队伍均停止行进.设排尾从位置![]() 开始行进的时间为
开始行进的时间为![]() ,排头与
,排头与![]() 的距离为
的距离为![]()
(1)当![]() 时,解答:
时,解答:
①求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围);
的取值范围);
②当甲赶到排头位置时,求![]() 的值;在甲从排头返回到排尾过程中,设甲与位置
的值;在甲从排头返回到排尾过程中,设甲与位置![]() 的距离为
的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
(2)设甲这次往返队伍的总时间为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围),并写出队伍在此过程中行进的路程.
的取值范围),并写出队伍在此过程中行进的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
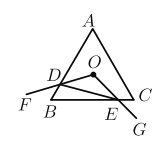
【题目】如图,等边三角形ABC的边长为4, 点O是![]() 的中心, ∠FOG = 120°, 绕点O旋转∠FOG,分别交线段AB、BC于D、 E两点,连接DE,给出下列四个结论:①OD= OE;②
的中心, ∠FOG = 120°, 绕点O旋转∠FOG,分别交线段AB、BC于D、 E两点,连接DE,给出下列四个结论:①OD= OE;②![]() ;③四边形ODBE的面积始终等于
;③四边形ODBE的面积始终等于![]() ;④
;④![]() 周长的最小值为6.上述结论中正确的有_________(写出序号)
周长的最小值为6.上述结论中正确的有_________(写出序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 ;
(2)当x 时,y随x的增大而减小;
(3)怎样移动抛物线![]() 就可以得到抛物线
就可以得到抛物线![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
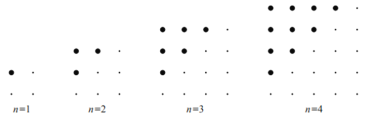
【题目】在下图中,每个正方形点阵由大点和小点组成:
(1)第7个正方形点阵中,大点和小点的总共的个数是________其中大点的个数是_________.
(2)第n个图形中,大点的个数是__________;(用含n的式子表示)
(3)是否存在某个图形,使得大点的个数是210个?若存在,请求出n的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com