
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,
,![]() ,其中
,其中![]() .下列四个结论:①
.下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,正确的个数是( )
,正确的个数是( )
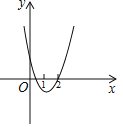
A.1B.2C.3D.4
【答案】C
【解析】
根据抛物线的开口方向、对称轴的位置、与y轴的交点可依次确定a、b、c的符号,进而可判断①;
根据对称轴的位置可得a、b的关系,再根据当![]() 时,
时,![]() ,把得出的a、b的关系式代入整理即可判断②;
,把得出的a、b的关系式代入整理即可判断②;
![]() 除以4可得
除以4可得![]() ,即为当
,即为当![]() 时
时![]() 的值,再结合图象判断
的值,再结合图象判断![]() 和x1的关系即可判断③;
和x1的关系即可判断③;
易判断![]() ,展开整理再结合
,展开整理再结合![]() 即可判断④.
即可判断④.
解:①∵抛物线开口向上,∴![]() ,
,
∵抛物线对称轴在![]() 轴的右侧,∴
轴的右侧,∴![]() ,
,
∵抛物线与![]() 轴的交点在
轴的交点在![]() 轴上方,∴
轴上方,∴![]() ,
,
∴![]() ,所以①正确;
,所以①正确;
②∵图象与![]() 轴交于两点
轴交于两点![]() ,
,![]() ,其中
,其中![]() ,
,
∴![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,
,
∵当![]() 时,
时,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,故②正确;
,故②正确;
③当![]() 时,
时,![]() 值为
值为![]() ,给
,给![]() 乘以4,即可化为
乘以4,即可化为![]() ,
,
∵当![]() 时,由图象可知在
时,由图象可知在![]() 和x1之间
和x1之间![]() 为正值,当
为正值,当![]() 时,在
时,在![]() 和x1之间
和x1之间![]() 为负值,∴
为负值,∴![]() 与0的关系不能确定,故③错误;
与0的关系不能确定,故③错误;
④∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
即![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() .
.
所以④正确.
综上,正确的是①②④,共3个,故选:C.


科目:初中数学 来源: 题型:
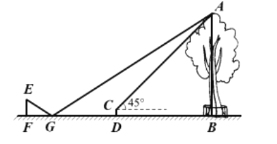
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
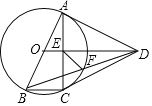
【题目】如图,CD是⊙O的直径,OB⊥CD交⊙O于点B,连接CB,AB是⊙O的弦,AB交CD于点E,F是CD的延长线上一点且AF=EF.

(1)判断AF和⊙O的位置关系并说明理由.
(2)若∠ABC=60°,BC=1cm,求阴影部分的面积.(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,过点B作直线EF∥AC,又知∠ACB=∠BDC=60°,AC=![]() cm.
cm.
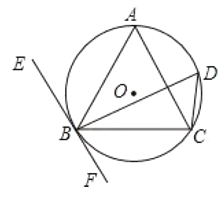
(1)请探究EF与⊙O的位置关系,并说明理由;
(2)求⊙O的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
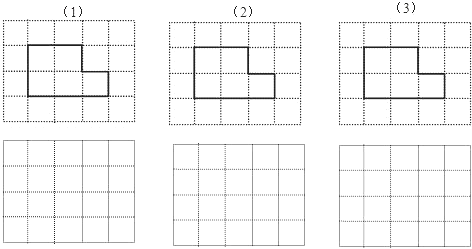
【题目】现有一块形如母子正方形的板材,木工师傅想先把它分割成几块,然后适当拼接,制成某种特殊形状的板面(要求板材不能有剩余,拼接时不重叠、无空隙),请你按下列要求,帮助木工师傅分别设计一种方案:
(1)板面形状为非正方形的中心对称图形;
(2)板面形状为等腰梯形;
(3)板面形状为正方形.
请在方格纸中的图形上画出分割线,在相应的下边的方格纸上面画出拼接后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
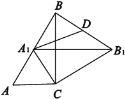
【题目】如图,RtΔABC中∠C=90°,∠ABC=30°,ΔABC绕点C顺时针旋转得ΔA1B1C,当A1落在AB上时,连接B1B,取B1B的中点D,连接A1D,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
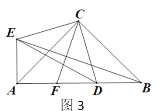
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C 顺时针旋转90°至CE,连接AE.
(1)求证:△BCD≌△ACE;
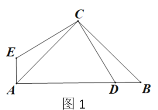
(2)如图2,连接ED,若CD=![]() ,AE=1,求AB的长;
,AE=1,求AB的长;
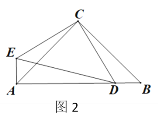
(3)如图3,若点F为AD的中点,分别连接EB和CF,求证:CF⊥EB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“心灵信箱”的设立,为师、生之间的沟通开设了一个书面交流的渠道.为了解九年级学生对“心灵信箱”开通两年来的使用情况,某课题组对该校九年级全体学生进行了一次问卷调查,并根据调查结果绘制了如下尚不完整的统计图.
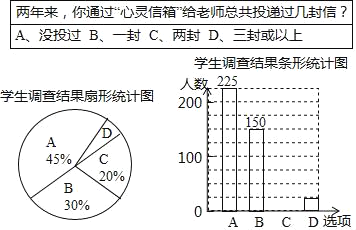
根据图表,解答以下问题:
(1)该校九年级学生共有 人;
(2)学生调查结果扇形统计图中,扇形D的圆心角度数是 ;
(3)请你补充条形统计图;
(4)根据调查结果可以推断:两年来,该校九年级学生通过“心灵信箱”投递出的信件总数至少有 封.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com