
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C 顺时针旋转90°至CE,连接AE.
(1)求证:△BCD≌△ACE;
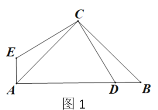
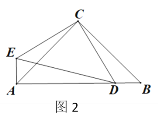
(2)如图2,连接ED,若CD=![]() ,AE=1,求AB的长;
,AE=1,求AB的长;
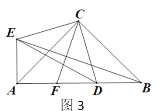
(3)如图3,若点F为AD的中点,分别连接EB和CF,求证:CF⊥EB.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据旋转的性质,利用SAS即可证明△BCD≌△ACE;
(2)由(1)可知AE=BD=1,证明∠EAD=90°,在Rt△ECD和Rt△EAD中,根据勾股定理,即可求得ED和AD,进而求得AB;
(3)过C作CG⊥AB于G,则AG=![]() AB,再证明
AB,再证明![]() ,
,![]() ,即可得出
,即可得出![]() ,且∠CGF=∠BAE=90°,证明出△CGF∽△BAE,得出∠FCG=∠ABE,即可证得∠ABE+∠CFG=90°,即CF⊥BE.
,且∠CGF=∠BAE=90°,证明出△CGF∽△BAE,得出∠FCG=∠ABE,即可证得∠ABE+∠CFG=90°,即CF⊥BE.
(1)由旋转性质可得EC=DC,∠ECD=90°=∠ACB,
∴∠BCD=∠ACE,
又∵AC=BC,
∴△BCD≌△ACE(SAS);
(2)由(1)可知AE=BD=1,∠CAE=∠B=45°=∠CAB,
∴∠EAD=90°,
∴![]() ,
,![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
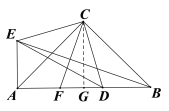
(3)如图,过C作CG⊥AB于G,则AG=![]() AB,
AB,
∵∠ACB=90°,AC=BC,
∴CG=![]() AB,即
AB,即![]() ,
,
∵点F为AD的中点,
∴FA=![]() AD,
AD,
∴FG=AG﹣AF,
=![]() AB﹣
AB﹣![]() AD=
AD=![]() (AB﹣AD)=
(AB﹣AD)=![]() BD,
BD,
由(1)可得:BD=AE,
∴FG=![]() AE,即
AE,即![]() ,
,
∴![]() ,
,
又∵∠CGF=∠BAE=90°,
∴△CGF∽△BAE,
∴∠FCG=∠ABE,
∵∠FCG+∠CFG=90°,
∴∠ABE+∠CFG=90°,
∴CF⊥BE.


科目:初中数学 来源: 题型:
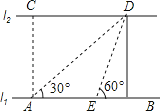
【题目】如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.求:C,D两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏州市某初中学校对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
时间(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |
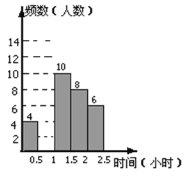
(1)a= ,b= ;
(2)补全频数分布直方图;
(3)请估计该校1 500名初中学生中,约有多少学生在1.5小时以内完成家庭作业.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行随机抽样的问卷调查,调查结果分为“![]() .非常了解”、“
.非常了解”、“![]() .了解”、“
.了解”、“![]() .基本了解”、“
.基本了解”、“![]() .不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.
.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.

(1)这次调查的市民人数为 人,图2中, ![]() ;
;
(2)补全图1中的条形统计图;
(3)在图2中的扇形统计图中,求“![]() .基本了解”所在扇形的圆心角度数;
.基本了解”所在扇形的圆心角度数;
(4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“![]() .不太了解”的市民约有多少万人?
.不太了解”的市民约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数(k>0,x>0)的图象经过AC的中点D,则k的值为( )
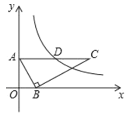
A.8B.5C.6D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的一次函数
的一次函数![]() 和反比例函数
和反比例函数![]() 的图像都经过点
的图像都经过点![]() .
.
求:(1)一次函数和反比例函数的解析式;
(2)若一次函数和反比例函数图像的另一个交点![]() 的坐标为
的坐标为![]() ,请结合图像直接写出
,请结合图像直接写出![]() 的
的![]() 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(满分7分)五月石榴红,枝头鸟儿歌.一只小鸟从石榴树上的A处沿直线飞到对面一房屋的顶部C处.从A处看房屋顶部C处的仰角为![]() ,看房屋底部D处的俯角为
,看房屋底部D处的俯角为![]() ,石榴树与该房屋之间的水平距离为
,石榴树与该房屋之间的水平距离为![]() 米,求出小鸟飞行的距离AC和房屋的高度CD.
米,求出小鸟飞行的距离AC和房屋的高度CD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com