【题目】（满分7分）五月石榴红，枝头鸟儿歌.一只小鸟从石榴树上的A处沿直线飞到对面一房屋的顶部C处.从A处看房屋顶部C处的仰角为
,看房屋底部D处的俯角为
,石榴树与该房屋之间的水平距离为
米，求出小鸟飞行的距离AC和房屋的高度CD.
【答案】解：作AE⊥CD于点E.
由题意可知：∠CAE =30°，∠EAD =45°，AE=
米. …………………1分
在Rt△ACE中，tan∠CAE=
，即tan30°=
.
∴CE=
=
(米)，……………………………………3分
∴AC=2CE=2×3 =6(米). ……………………………………………………4分
在Rt△AED中，∠ADE=90°-∠EAD =90°-45°= 45°，
∴DE=AE=
(米). ………………………………………………………5分
∴DC=CE+DE=（3+）米. ……………………………………………6分
答：AC=6米，DC=（3+）米. …………………………………………7分
【解析】略
科目：初中数学 来源： 题型：
【题目】如图1，在△ABC中，∠ACB=90°，AC=BC，D为AB上一点，连接CD，将CD绕点C 顺时针旋转90°至CE，连接AE．
（1）求证：△BCD≌△ACE；
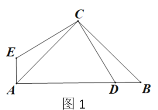
（2）如图2，连接ED，若CD=
，AE=1，求AB的长；
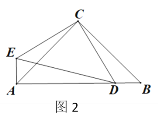
（3）如图3，若点F为AD的中点，分别连接EB和CF，求证：CF⊥EB．
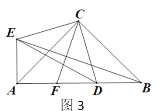
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校“心灵信箱”的设立，为师、生之间的沟通开设了一个书面交流的渠道．为了解九年级学生对“心灵信箱”开通两年来的使用情况，某课题组对该校九年级全体学生进行了一次问卷调查，并根据调查结果绘制了如下尚不完整的统计图．
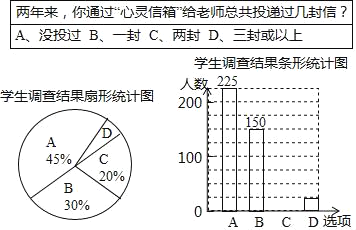
根据图表，解答以下问题：
（1）该校九年级学生共有 人；
（2）学生调查结果扇形统计图中，扇形D的圆心角度数是 ；
（3）请你补充条形统计图；
（4）根据调查结果可以推断：两年来，该校九年级学生通过“心灵信箱”投递出的信件总数至少有 封．
查看答案和解析>>
科目：初中数学 来源： 题型：
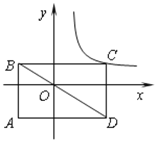
【题目】如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数
的图象上，AB与x轴交于点E，BE:AE=1:2．若点B的坐标为（－2，1），则k的值为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
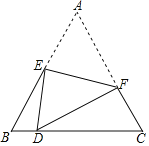
【题目】在等边△ABC中，AB＝5，点D为BC上一点，BD：DC＝1：4．点E和点F分别是AB、AC边上的点，将△AEF沿EF折叠，使点A刚好落在点D处，则AF＝_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在初中数学学习阶段，我们常常会利用一些变形技巧来简化式子，解答问题．
材料一：在解决某些分式问题时，倒数法是常用的变形技巧之一．所谓倒数法，即把式子变成其倒数形式，从而运用约分化简，以达到计算目的．
例：已知：
，求代数式
的值．
解：∵，∴
即
，∴
，∴
．
材料二：在解决某些连等式问题时，通常可以引入参数“k”，将连等式变成几个值为k的等式，这样就可以通过适当变形解决问题．
例：若2x＝3y＝4z，且xyz≠0，求
的值．
解：令2x＝3y＝4z＝k（k≠0）
则
，
，
，∴
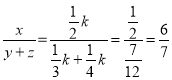
根据材料回答问题：
（1）已知
，则
＝ ；
（2）解分式方程组：
；
（3）若
，x≠0，y≠0，z≠0，且abc＝5，求xyz的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点
、
在
轴上，点
在
轴上，
，
，
为线段
上一动点，以
为边在轴上方作正方形
，连接
．
（1）若点的坐标为
，则
________；
（2）当
________时，
轴；
（3）当点由点运动到点过程中，点
经过的路径长为________；
（4）当
面积最大时，求出
的长及面积最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题发现：
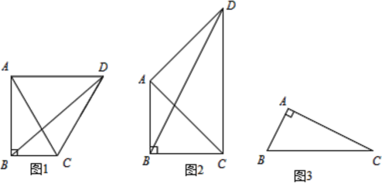
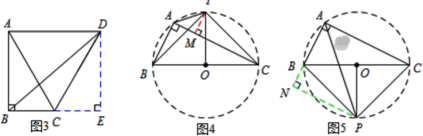
（1）如图1，在Rt△ABC中，∠BAC=30°，∠ABC＝90°，将线段AC绕点A逆时针旋转，旋转角α=2∠BAC， ∠BCD的度数是 ；线段BD，AC之间的数量关系是 ．
类比探究：
（2）在Rt△ABC中，∠BAC=45°，∠ABC＝90°，将线段AC绕点A逆时针旋转，旋转角α=2∠BAC，请问（1）中的结论还成立吗？；
拓展延伸：
（3）如图3，在Rt△ABC中，AB＝2，AC＝4，∠BDC＝90°，若点P满足PB＝PC，∠BPC＝90°，请直接写出线段AP的长度．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
