
【题目】如图,正方形ABCD的边长为2,点E是边AD的中点,以EC为边作正方形CEFG,则点D与点F之间的距离等于________

【答案】![]() 或
或![]()
【解析】
可分两种情况讨论:①当正方形CEFG在CE的右侧时,如图,过点F作FH⊥AD,交AD的延长线于点H,通过证明△EFH≌△CED求出DH、HF的值,再根据勾股定理求解即可;②当正方形CEFG在CE的左侧时,如图,过点F作FH⊥DA,交DA的延长线于点H,通过证明△EFH≌△CED求出DH、HF的值,再根据勾股定理求解即可.
可分当正方形CEFG在CE的右侧和左侧两种情况讨论:
①当正方形CEFG在CE的右侧时,如图,过点F作FH⊥AD,交AD的延长线于点H,
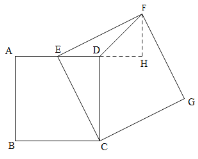
∵E是AD的中点,
∴DE= ![]() AD=1,
AD=1,
∵∠FEC=∠ADC=90°,
∴∠FEH+∠CED=∠CED+∠DCE=90°,
∴∠FEH=∠DCE,
∵∠EHF=∠CDE=90°,CE=EF,
∴△EFH≌△CED(AAS),
∴FH=DE=1,HE=CD=2,
∴HD=1,
∴![]() ;
;
②当正方形CEFG在CE的左侧时,如图,过点F作FH⊥DA,交DA的延长线于点H,
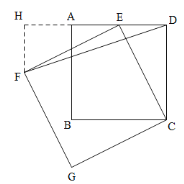
∵E是AD的中点,
∴AE= ![]() AD=1,
AD=1,
∵∠FEC=∠CDE=90°,
∴∠FEH+∠CED=∠CED+∠DCE=90°,
∴∠FEH=∠DCE,
∵∠EHF=∠CDE=90°,CE=EF,
∴△EFH≌△CED(AAS),
∴FH=DE=1,HE=CD=2,
∴HD=HE+DE=3,
∴![]() ;
;
故答案为:![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】苏州市某初中学校对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业时间不超过1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
时间(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |
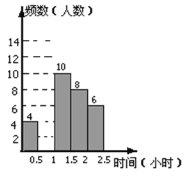
(1)a= ,b= ;
(2)补全频数分布直方图;
(3)请估计该校1 500名初中学生中,约有多少学生在1.5小时以内完成家庭作业.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的一次函数
的一次函数![]() 和反比例函数
和反比例函数![]() 的图像都经过点
的图像都经过点![]() .
.
求:(1)一次函数和反比例函数的解析式;
(2)若一次函数和反比例函数图像的另一个交点![]() 的坐标为
的坐标为![]() ,请结合图像直接写出
,请结合图像直接写出![]() 的
的![]() 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
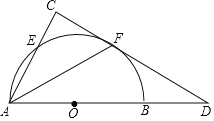
【题目】如图,已知AB是⊙O的直径,⊙O与Rt△ACD的两直角边分别交于点E、F,点F是弧BE的中点,∠C=90°,连接AF.
(1)求证:直线DF是⊙O的切线.
(2)若BD=1,OB=2,求tan∠AFC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“我为武汉加油”征文活动中,学校计划对获得一、二等奖的学生分别奖励一台计算器,一个考试包.已知购买![]() 台计算器和
台计算器和![]() 个考试包共
个考试包共![]() 元,购买
元,购买![]() 台计算器和
台计算器和![]() 个考试包共
个考试包共![]() 元.
元.
(1)计算器、考试包的单价分别为多少元?
(2)经与商家协商,购买计算器超过![]() 台时,每增加一台,单价降低
台时,每增加一台,单价降低![]() 元;超过
元;超过![]() 台,均按购买
台,均按购买![]() 台的单价销售,考试包一律按原价销售,学校计划奖励一、等奖学生共计
台的单价销售,考试包一律按原价销售,学校计划奖励一、等奖学生共计![]() 人,其中一等奖的人数不少于
人,其中一等奖的人数不少于![]() 人,且不超过
人,且不超过![]() 人,这次奖励一等奖学生多少人时,购买奖品金额最少,最少为多少元?
人,这次奖励一等奖学生多少人时,购买奖品金额最少,最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(满分7分)五月石榴红,枝头鸟儿歌.一只小鸟从石榴树上的A处沿直线飞到对面一房屋的顶部C处.从A处看房屋顶部C处的仰角为![]() ,看房屋底部D处的俯角为
,看房屋底部D处的俯角为![]() ,石榴树与该房屋之间的水平距离为
,石榴树与该房屋之间的水平距离为![]() 米,求出小鸟飞行的距离AC和房屋的高度CD.
米,求出小鸟飞行的距离AC和房屋的高度CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A1的坐标为(2,4),以点O为圆心,以OA1长为半径画弧,交直线y=x于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2,以O为圆心,以OA2长为半径画弧,交直线y=x于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3,以点O为圆心,以OA3长为半径画弧,交直线y=x于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4,以点O为圆心,以OA4长为半径画弧,交直线y=x于点B4,…按照如此规律进行下去,点B2020的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复课返校后,为了拉大学生锻炼的间距,学校决定增购适合独立训练的两种体育器材:跳绳和毽子.如果购进5根跳绳和6个毽子共需196元;购进2根跳绳和5个键子共需120元.
(1)求一根跳绳和一个毽子的售价分别是多少元;
(2)学校计划购买跳绳和键子两种器材共400个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于310根,请你求出学校花钱最少的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com