
【题目】在“我为武汉加油”征文活动中,学校计划对获得一、二等奖的学生分别奖励一台计算器,一个考试包.已知购买![]() 台计算器和
台计算器和![]() 个考试包共
个考试包共![]() 元,购买
元,购买![]() 台计算器和
台计算器和![]() 个考试包共
个考试包共![]() 元.
元.
(1)计算器、考试包的单价分别为多少元?
(2)经与商家协商,购买计算器超过![]() 台时,每增加一台,单价降低
台时,每增加一台,单价降低![]() 元;超过
元;超过![]() 台,均按购买
台,均按购买![]() 台的单价销售,考试包一律按原价销售,学校计划奖励一、等奖学生共计
台的单价销售,考试包一律按原价销售,学校计划奖励一、等奖学生共计![]() 人,其中一等奖的人数不少于
人,其中一等奖的人数不少于![]() 人,且不超过
人,且不超过![]() 人,这次奖励一等奖学生多少人时,购买奖品金额最少,最少为多少元?
人,这次奖励一等奖学生多少人时,购买奖品金额最少,最少为多少元?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
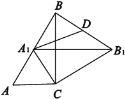
【题目】如图,RtΔABC中∠C=90°,∠ABC=30°,ΔABC绕点C顺时针旋转得ΔA1B1C,当A1落在AB上时,连接B1B,取B1B的中点D,连接A1D,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“心灵信箱”的设立,为师、生之间的沟通开设了一个书面交流的渠道.为了解九年级学生对“心灵信箱”开通两年来的使用情况,某课题组对该校九年级全体学生进行了一次问卷调查,并根据调查结果绘制了如下尚不完整的统计图.
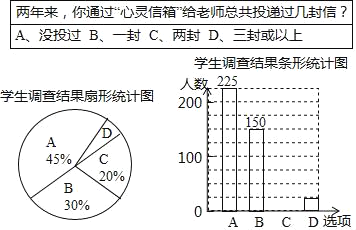
根据图表,解答以下问题:
(1)该校九年级学生共有 人;
(2)学生调查结果扇形统计图中,扇形D的圆心角度数是 ;
(3)请你补充条形统计图;
(4)根据调查结果可以推断:两年来,该校九年级学生通过“心灵信箱”投递出的信件总数至少有 封.
查看答案和解析>>
科目:初中数学 来源: 题型:
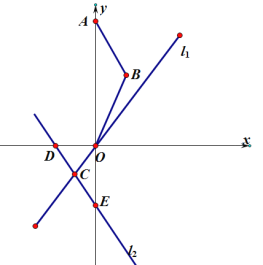
【题目】已知抛物线y=x2+bx+c经过点A(0,6),点B(1,3),直线l1:y=kx(k≠0),直线l2:y=-x-2,直线l1经过抛物线y=x2+bx+c的顶点P,且l1与l2相交于点C,直线l2与x轴、y轴分别交于点D、E.若把抛物线上下平移,使抛物线的顶点在直线l2上(此时抛物线的顶点记为M),再把抛物线左右平移,使抛物线的顶点在直线l1上(此时抛物线的顶点记为N).
(1)求抛物y=x2+bx+c线的解析式.
(2)判断以点N为圆心,半径长为4的圆与直线l2的位置关系,并说明理由.
(3)设点F、H在直线l1上(点H在点F的下方),当△MHF与△OAB相似时,求点F、H的坐标(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
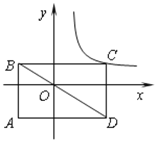
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上,AB与x轴交于点E,BE:AE=1:2.若点B的坐标为(-2,1),则k的值为________.
的图象上,AB与x轴交于点E,BE:AE=1:2.若点B的坐标为(-2,1),则k的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一.所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式
,求代数式![]() 的值.
的值.
解:∵![]() ,∴
,∴![]()
即![]() ,∴
,∴![]() ,∴
,∴![]() .
.
材料二:在解决某些连等式问题时,通常可以引入参数“k”,将连等式变成几个值为k的等式,这样就可以通过适当变形解决问题.
例:若2x=3y=4z,且xyz≠0,求![]() 的值.
的值.
解:令2x=3y=4z=k(k≠0)
则![]() ,
,![]() ,
,![]() ,∴
,∴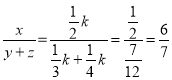
根据材料回答问题:
(1)已知![]() ,则
,则![]() = ;
= ;
(2)解分式方程组: ;
;
(3)若![]() ,x≠0,y≠0,z≠0,且abc=5,求xyz的值.
,x≠0,y≠0,z≠0,且abc=5,求xyz的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
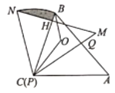
【题目】如图,两个三角形纸板![]() ,
,![]() 能完全重合,
能完全重合,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 从重合位置开始,按逆时针方向旋转,边
从重合位置开始,按逆时针方向旋转,边![]() ,
,![]() 分别与
分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合),点
重合),点![]() 是
是![]() 的内心,若
的内心,若![]() ,点
,点![]() 运动的路径为
运动的路径为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com