
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.
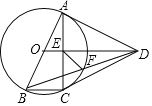
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】(1)连接OC,证△OAD≌△OCD得∠ADO=∠CDO,由AD=CD知DE⊥AC,再由AB为直径知BC⊥AC,从而得OD∥BC;
(2)根据tan∠ABC=2可设BC=a、则AC=2a、AD=AB=![]() ,证OE为中位线知OE=
,证OE为中位线知OE=![]() a、AE=CE=
a、AE=CE=![]() AC=a,进一步求得DE=
AC=a,进一步求得DE=![]() =2a,在△AOD中利用勾股定理逆定理证∠OAD=90°即可得;
=2a,在△AOD中利用勾股定理逆定理证∠OAD=90°即可得;
(3)先证△AFD∽△BAD得DFBD=AD2①,再证△AED∽△OAD得ODDE=AD2②,由①②得DFBD=ODDE,即![]() ,结合∠EDF=∠BDO知△EDF∽△BDO,据此可得
,结合∠EDF=∠BDO知△EDF∽△BDO,据此可得![]() ,结合(2)可得相关线段的长,代入计算可得.
,结合(2)可得相关线段的长,代入计算可得.
(1)如图,连接OC,
在△OAD和△OCD中,
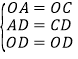 ,
,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
又AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACB=90°,即BC⊥AC,
∴OD∥BC;
(2)∵tan∠ABC=![]() =2,
=2,
∴设BC=a、则AC=2a,
∴AD=AB=![]() ,
,
∵OE∥BC,且AO=BO,
∴OE=![]() BC=
BC=![]() a,AE=CE=
a,AE=CE=![]() AC=a,
AC=a,
在△AED中,DE=![]() =2a,
=2a,
在△AOD中,AO2+AD2=(![]() )2+(
)2+(![]() a)2=
a)2=![]() a2,
a2,
OD2=(OF+DF)2=(![]() a+2a)2=
a+2a)2=![]() a2,
a2,
∴AO2+AD2=OD2,
∴∠OAD=90°,
则DA与⊙O相切;
(3)如图,连接AF,
∵AB是⊙O的直径,
∴∠AFD=∠BAD=90°,
∵∠ADF=∠BDA,
∴△AFD∽△BAD,
∴![]() ,即DFBD=AD2①,
,即DFBD=AD2①,
又∵∠AED=∠OAD=90°,∠ADE=∠ODA,
∴△AED∽△OAD,
∴![]() ,即ODDE=AD2②,
,即ODDE=AD2②,
由①②可得DFBD=ODDE,即![]() ,
,
又∵∠EDF=∠BDO,
∴△EDF∽△BDO,
∴![]() ,
,
∵BC=1,
∴AB=AD=![]() 、OD=
、OD=![]() 、ED=2、BD=
、ED=2、BD=![]() 、OB=
、OB=![]() ,
,
∴![]() ,
,
∴EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,AD=DC,点F在AD上,AB=FC,BF的延长线交AC于点E.
(1)求证:△ABD≌△CFD.
(2)求证:CF⊥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索题:
(x-1)(x+1)=x![]() -1
-1
(x-1)(x![]() +x+1)=x
+x+1)=x![]() -1
-1
(x-1)(x![]() +x
+x![]() +x+1)=x
+x+1)=x![]() -1
-1
(x-1)(x![]() + x
+ x![]() +x
+x![]() +x+1)=x
+x+1)=x![]() -1
-1
(1)观察以上各式并猜想:
①(x-1)(x![]() +x
+x![]() +x
+x![]() + x
+ x![]() +x
+x![]() +x+1)= ;
+x+1)= ;
②(x-1)(x![]() +x
+x![]() +x
+x![]() +… x
+… x![]() +x
+x![]() +x+1)= ;
+x+1)= ;
(2)请利用上面的结论计算:
①(-2)![]() +(-2)
+(-2)![]() +(-2)
+(-2)![]() +…+(-2)+1
+…+(-2)+1
②若 x![]() +x
+x![]() +…+x
+…+x![]() +x
+x![]() +x+1=0,求 x
+x+1=0,求 x![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
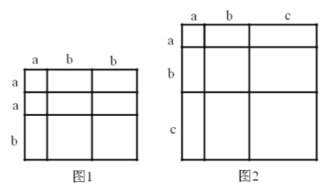
【题目】阅读下列文字,对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如:由图1可以得到![]() ,请解答下列问题:
,请解答下列问题:
(1)写出图2中所表示的数学等式 ;
(2)利用(1)中所得到的结论,解决问题:已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
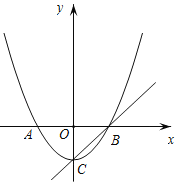
【题目】如图,已知顶点为C(0,﹣3)的抛物线y=ax2+b(a≠0)与x轴交于A,B两点,直线y=x+m过顶点C和点B.
(1)求m的值;
(2)求函数y=ax2+b(a≠0)的解析式;
(3)抛物线上是否存在点M,使得∠MCB=15°?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
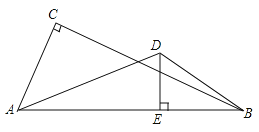
【题目】如图,学校位于高速路AB的一侧(AB成一条直线),点A,B为高速路上距学校直线距离最近的2个隧道出入口,点C、D为学校的两栋教学楼,经测量∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,点D到高速路的最短直线距离DE=400m.
(1)求教学楼C到隧道口B的直线距离;
(2)比较AC2+BC2与AD2+BD2谁大谁小,试用计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为( )

A. ![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车司机某天在东西方向的公路上营运,往东行驶的路程记作正数,往西行驶的路程记作负数.全天行程的记录如下:30,-28,-13,15,27,-30,45,-27;(单位:千米)
(1)当小张将最后一位乘客送到目的地时,距出发地点的距离为多少千米?
(2)若每千米的营业额为7元,则小张这天的总营业额为多少元?
(3)在(2)的情况下,如果营运成本为每千米2元,那么这天盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
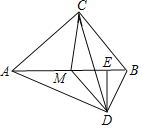
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,点M是斜边AB的中点,MD∥BC,且MD=CM,DE⊥AB于点E,连结AD、CD.
(1)求证:△MED∽△BCA;
(2)求证:△AMD≌△CMD;
(3)设△MDE的面积为S1,四边形BCMD的面积为S2,当S2=![]() S1时,求cos∠ABC的值.
S1时,求cos∠ABC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com