
【题目】探索题:
(x-1)(x+1)=x![]() -1
-1
(x-1)(x![]() +x+1)=x
+x+1)=x![]() -1
-1
(x-1)(x![]() +x
+x![]() +x+1)=x
+x+1)=x![]() -1
-1
(x-1)(x![]() + x
+ x![]() +x
+x![]() +x+1)=x
+x+1)=x![]() -1
-1
(1)观察以上各式并猜想:
①(x-1)(x![]() +x
+x![]() +x
+x![]() + x
+ x![]() +x
+x![]() +x+1)= ;
+x+1)= ;
②(x-1)(x![]() +x
+x![]() +x
+x![]() +… x
+… x![]() +x
+x![]() +x+1)= ;
+x+1)= ;
(2)请利用上面的结论计算:
①(-2)![]() +(-2)
+(-2)![]() +(-2)
+(-2)![]() +…+(-2)+1
+…+(-2)+1
②若 x![]() +x
+x![]() +…+x
+…+x![]() +x
+x![]() +x+1=0,求 x
+x+1=0,求 x![]() 的值.
的值.
【答案】(1)①x7-1,②xn+1-1;(2)①![]() ,②1.
,②1.
【解析】
(1)①②根据已知式子进行探寻规律即可;
(2)①将原始乘以(-2-1)后除以(-2-1),再运用公式计算即可;
②将原始乘以(x-1)后除以(x-1),再运用公式计算即可.
(1)①(x-1)(x6+x5+x4+x3+x2+x+1)=x7-1,
②(x-1)(xn+xn-1+xn-2+…+x3+x2+x+1)=xn+1-1,
故答案为x7-1,xn+1-1;
(2)①(-2)50+(-2)49+(-2)48+…+(-2)+1=
=(-2-1)×[(-2)50+(-2)49+(-2)48+…+(-2)+1]÷(-2-1)
=[(-2)51-1]÷(-3)
=(-251-1)÷(-3)
=![]() ,
,
②x1007+x1006+…+x3+x2+x+1
=(x-1)(x1007+x1006+…+x3+x2+x+1)÷(x-1)
=(x1008-1)÷(x-1),
∴x1008-1=0,
x1008=1,
∴x3024=(x1008)3=1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
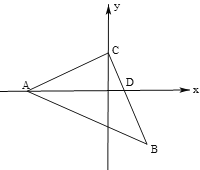
【题目】在平面直角坐标系中,三角形△ABC为等腰直角三角形,AC=BC,BC交x轴于点D.
(1)若A(-4,0),C(0,2),求点B的坐标;
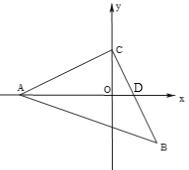
(2)若∠EDB=∠ADC,问∠ADE与∠CAD满足怎样的关系?并证明.
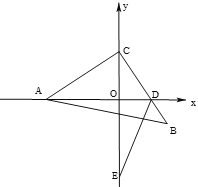
(3)若AD平分∠BAC,A(-4,0),D(m,0),B的纵坐标为n,试探究m、n之间满足怎样的关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
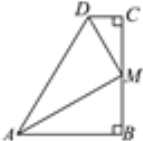
【题目】如图所示,已知∠B=∠C=90°,AM平分∠DAB,DM平分∠ADC.
(1)求证:M是BC的中点.
(2) 求证:AD=AB+CD.
(3)S△AMD=______S四边形ABCD.
查看答案和解析>>
科目:初中数学 来源: 题型:
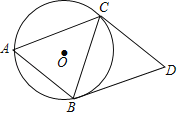
【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=![]() ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
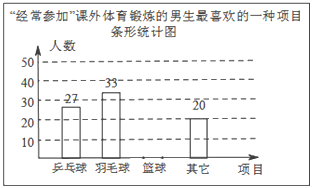
【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如图两幅尚不完整的统计图.请根据以上信息解答下列问题:
①课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为_________.
②请补全条形统计图.
③该校共有1500名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A坐标为(2,0),点B在x轴负半轴上,C在y轴正半轴上,∠ACB=90°,∠ABC=30°.
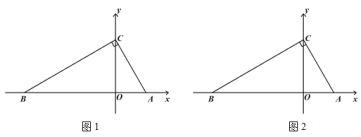
(1)求点B坐标;
(2)如图2,点P从B出发,沿线段BC运动,点P运动速度为每秒2个单位长度,设运动时间为t秒,用含t的式子表示三角形△OBP的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能:
① AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;
② AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;
③ AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
④ AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.
其中能判定四边形ABCD和四边形A1B1C1D1全等有( )个

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
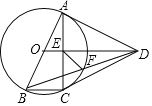
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
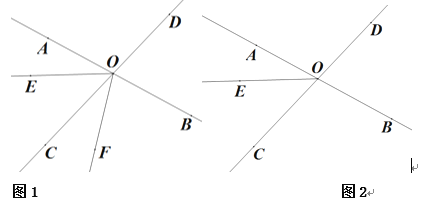
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE=![]() ∠EOC
∠EOC
(1)求∠AOE的度数;
(2)将射线OE绕点O逆时针旋转![]() °(0°<α<360°)到OF.
°(0°<α<360°)到OF.
①如图2,当OF平分∠BOE时,求∠DOF的度数;
②若∠AOF=120°时,直接写出![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com