
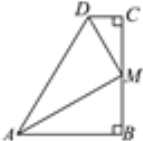
【题目】如图所示,已知∠B=∠C=90°,AM平分∠DAB,DM平分∠ADC.
(1)求证:M是BC的中点.
(2) 求证:AD=AB+CD.
(3)S△AMD=______S四边形ABCD.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
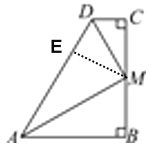
(1)过点M作ME⊥AD交AD于点E,根据角平分线的性质定理可得ME=MB,ME=MC,等量代换得到MB=MC即可证明;
(2)利用HL易证Rt△AEM≌Rt△ABM,Rt△DCM≌Rt△DEM,可得AD=AE+DE=AB+CD;
(3)利用三角形全等的性质得到S△AEM=S△ABM,S△DCM=S△DEM,即可求出S△AMD=S△AEM+S△DEM=![]() S四边形ABCD.
S四边形ABCD.
解:(1)过点M作ME⊥AD交AD于点E,
∵∠B=∠C=90°,
∴MB⊥AB,MC⊥DC,
又∵AM平分∠DAB,DM平分∠ADC,ME⊥AE,ME⊥DE,
∴ME=MB,ME=MC,
∴MB=MC,即M是BC的中点;
(2)在Rt△AEM和Rt△ABM中,![]() ,
,
∴Rt△AEM≌Rt△ABM(HL),
∴AE=AB,
同理可证Rt△DCM≌Rt△DEM,
∴DC=DE,
∴AD=AE+DE=AB+CD;
(3)由(2)可知Rt△AEM≌Rt△ABM,Rt△DCM≌Rt△DEM,
∴S△AEM=S△ABM,S△DCM=S△DEM,
∴S△AMD=S△AEM+S△DEM=![]() S四边形ABCD.
S四边形ABCD.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )
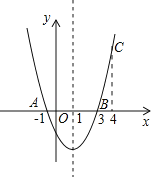
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,AD=DC,点F在AD上,AB=FC,BF的延长线交AC于点E.
(1)求证:△ABD≌△CFD.
(2)求证:CF⊥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角板的直角顶点C叠放在一起.

(1)若∠DCE=30°,求∠ACB的度数;
(2)试判断∠ACE与∠BCD的大小关系,并说明理由;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华与爸爸用一个如图所示的五等分、可以自由转动的转盘来玩游戏;将转盘随机转一次,指针指向的数字如果是奇数.爸爸获胜,如果是偶数,则小华获胜(指针指到线上则重转)
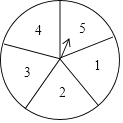
(1)转完转盘后指针指向数字2的概率是多少?
(2)这个游戏公平吗?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,等边△ABC中,D、E分别在BC、AC边上运动,且始终保持BD=CE,点D、E始终不与等边△ABC的顶点重合.连接AD、BE,AD、BE交于点F.
(1)写出在运动过程中始终全等的三角形,井选择其中一组证明;
(2)运动过程中,∠BFD的度数是否会改变?如果改变,请说明理由;如果不变,求出∠BFD的度数,再说明理由.
(3)直接写出运动过程中,AE、AB、BD三条线段长度之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索题:
(x-1)(x+1)=x![]() -1
-1
(x-1)(x![]() +x+1)=x
+x+1)=x![]() -1
-1
(x-1)(x![]() +x
+x![]() +x+1)=x
+x+1)=x![]() -1
-1
(x-1)(x![]() + x
+ x![]() +x
+x![]() +x+1)=x
+x+1)=x![]() -1
-1
(1)观察以上各式并猜想:
①(x-1)(x![]() +x
+x![]() +x
+x![]() + x
+ x![]() +x
+x![]() +x+1)= ;
+x+1)= ;
②(x-1)(x![]() +x
+x![]() +x
+x![]() +… x
+… x![]() +x
+x![]() +x+1)= ;
+x+1)= ;
(2)请利用上面的结论计算:
①(-2)![]() +(-2)
+(-2)![]() +(-2)
+(-2)![]() +…+(-2)+1
+…+(-2)+1
②若 x![]() +x
+x![]() +…+x
+…+x![]() +x
+x![]() +x+1=0,求 x
+x+1=0,求 x![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为( )

A. ![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com