
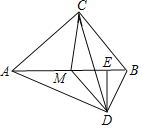
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,点M是斜边AB的中点,MD∥BC,且MD=CM,DE⊥AB于点E,连结AD、CD.
(1)求证:△MED∽△BCA;
(2)求证:△AMD≌△CMD;
(3)设△MDE的面积为S1,四边形BCMD的面积为S2,当S2=![]() S1时,求cos∠ABC的值.
S1时,求cos∠ABC的值.
【答案】(1)证明见解析;(2)证明见解析;(3)cos∠ABC=![]() .
.
【解析】
(1)易证∠DME=∠CBA,∠ACB=∠MED=90°,从而可证明△MED∽△BCA;
(2)由∠ACB=90°,点M是斜边AB的中点,可知MB=MC=AM,从而可证明∠AMD=∠CMD,从而可利用全等三角形的判定证明△AMD≌△CMD;
(3)易证MD=2AB,由(1)可知:△MED∽△BCA,所以![]() ,所以S△MCB=
,所以S△MCB=![]() S△ACB=2S1,从而可求出S△EBD=S2﹣S△MCB﹣S1=
S△ACB=2S1,从而可求出S△EBD=S2﹣S△MCB﹣S1=![]() S1,由于
S1,由于![]() ,从而可知
,从而可知![]() ,设ME=5x,EB=2x,从而可求出AB=14x,BC=
,设ME=5x,EB=2x,从而可求出AB=14x,BC=![]() ,最后根据锐角三角函数的定义即可求出答案.
,最后根据锐角三角函数的定义即可求出答案.
(1)∵MD∥BC,
∴∠DME=∠CBA,
∵∠ACB=∠MED=90°,
∴△MED∽△BCA;
(2)∵∠ACB=90°,点M是斜边AB的中点,
∴MB=MC=AM,
∴∠MCB=∠MBC,
∵∠DMB=∠MBC,
∴∠MCB=∠DMB=∠MBC,
∵∠AMD=180°﹣∠DMB,
∠CMD=180°﹣∠MCB﹣∠MBC+∠DMB=180°﹣∠MBC,
∴∠AMD=∠CMD,
在△AMD与△CMD中,
 ,
,
∴△AMD≌△CMD(SAS);
(3)∵MD=CM,
∴AM=MC=MD=MB,
∴MD=2AB,
由(1)可知:△MED∽△BCA,
∴![]() ,
,
∴S△ACB=4S1,
∵CM是△ACB的中线,
∴S△MCB=![]() S△ACB=2S1,
S△ACB=2S1,
∴S△EBD=S2﹣S△MCB﹣S1=![]() S1,
S1,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设ME=5x,EB=2x,
∴MB=7x,
∴AB=2MB=14x,
∵![]() ,
,
∴BC=10x,
∴cos∠ABC=![]() .
.


科目:初中数学 来源: 题型:
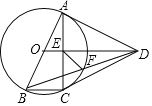
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC,OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交于⊙O于点F,连接EF,若BC=1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
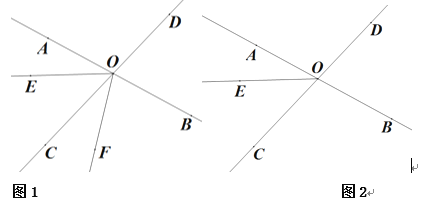
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE=![]() ∠EOC
∠EOC
(1)求∠AOE的度数;
(2)将射线OE绕点O逆时针旋转![]() °(0°<α<360°)到OF.
°(0°<α<360°)到OF.
①如图2,当OF平分∠BOE时,求∠DOF的度数;
②若∠AOF=120°时,直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(![]() ,
,![]() m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
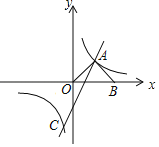
【题目】如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=![]() 交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
(1)求双曲线的解析式;
(2)求点C的坐标,并直接写出y1<y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条直线 m 将如图 1 的直角铁皮分成面积相等的两部分.图 2、图 3 分别是甲、乙两同学给出的作法,对于两人的作法判断正确的是( )
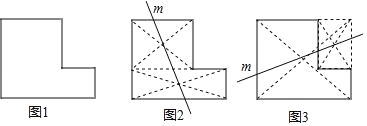
A. 甲正确,乙不正确B. 甲不正确,乙正确
C. 甲、乙都正确D. 甲、乙都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上.
上.
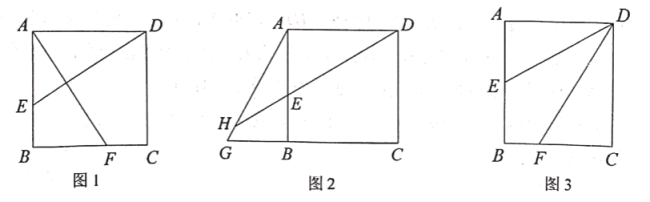
(1)若![]() ,
,![]() .
.
①如图1,求证:![]() ;
;
②如图2,点![]() 为
为![]() 延长线上一点,
延长线上一点,![]() 的延长线交
的延长线交![]() 于
于![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(2)如图3,若![]() 为
为![]() 的中点,
的中点,![]() .则
.则![]() 的值为 (结果用含
的值为 (结果用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应大括号里:![]() ,
,![]() 、-(-10) 、 -(-2)2,0.1010010001…
、-(-10) 、 -(-2)2,0.1010010001…
(1)正数集合{ …}
(2)整数集合{ …}
(3)正分数集合{ …}
(4)非负整数集合{ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小梅在餐厅吃饭时,发现了一个有趣的问题:厨师喜欢将做好的油饼都切成一个个小扇形.小梅在想:如果第一次切去圆饼的一半,第二次切去剩余的一半,第三次继续切去剩余的一半,……如图所示.
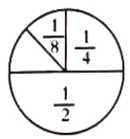
(1)如果继续这样切下去,能把这张油饼切完吗?为什么?
(2)如果依照上面的规律切了10次,那么剩下的油饼是整张油饼的几分之几?
(3)如果厨师照上述方式切了![]() 次,那么他一共将这张油饼切去了多少?
次,那么他一共将这张油饼切去了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com