【题目】用一条直线 m 将如图 1 的直角铁皮分成面积相等的两部分．图 2、图 3 分别是甲、乙两同学给出的作法，对于两人的作法判断正确的是（ ）
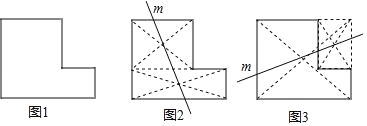
A. 甲正确，乙不正确B. 甲不正确，乙正确
C. 甲、乙都正确D. 甲、乙都不正确
阅读快车系列答案科目：初中数学 来源： 题型：
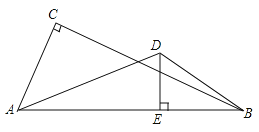
【题目】如图，学校位于高速路AB的一侧（AB成一条直线），点A，B为高速路上距学校直线距离最近的2个隧道出入口，点C、D为学校的两栋教学楼，经测量∠ACB=90°，∠ADB＞90°，AC=600m，AB=1000m，点D到高速路的最短直线距离DE=400m.
（1）求教学楼C到隧道口B的直线距离；
（2）比较AC2+BC2与AD2+BD2谁大谁小，试用计算说明.
查看答案和解析>>
科目：初中数学 来源： 题型：
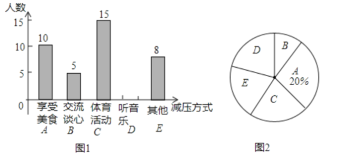
【题目】某校初三（1）班同学接受一次内容为“最适合自己的考前减压方式”的调查活动，收集整理数据后，老师将减压方式分为五类，并绘制了图1，图2两个不完整的统计图，请根据图中的信息解答下列问题．
（1）初三（1）班共有多少名同学？
（2）补全条形统计图，并标上相应的人数
（3）计算扇形统计图中的“其他
”所对应的圆心角度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，等腰直角三角形OAA1的直角边OA在x轴上，点A1在第一象限，且OA=1，以点A1为直角顶点，OA1为一直角边作等腰直角三角形OA1A2，再以点A2为直角顶点，OA2为直角边作等腰直角三角形OA2A3…依此规律，则点A2018的坐标是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
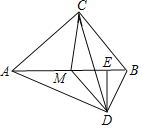
【题目】已知：如图，在Rt△ABC中，∠ACB=90°，点M是斜边AB的中点，MD∥BC，且MD=CM，DE⊥AB于点E，连结AD、CD．
（1）求证：△MED∽△BCA；
（2）求证：△AMD≌△CMD；
（3）设△MDE的面积为S1，四边形BCMD的面积为S2，当S2=
S1时，求cos∠ABC的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在图中网格上按要求画出图形，并回答问题：
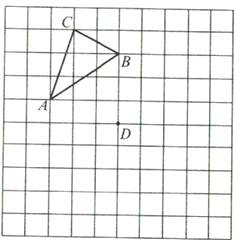
（1）如果将三角形
平移，使得点
平移到图中点
位置，点
、点
的对应点分别为点
、点
，请画出三角形
；
（2）画出三角形关于点成中心对称的三角形
．
（3）三角形与三角形______（填“是”或“否”）关于某个点成中心对称？如果是，请在图中画出这个对称中心，并记作点
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图，已知△ABC≌△DBE，点D在AC上，BC与DE交于点P，若AD=DC=2.4，BC=4.1．
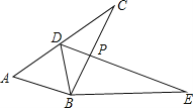
（1）若∠ABE=162°，∠DBC=30°，求∠CBE的度数；
（2）求△DCP与△BPE的周长和．
查看答案和解析>>
科目：初中数学 来源： 题型：
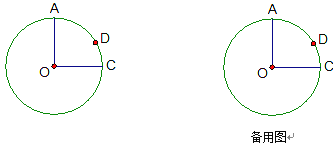
【题目】如图，⊙O的半径OA⊥OC，点D在
上，且
＝2
，OA＝4．
（1）∠COD＝ °；
（2）求弦AD的长；
（3）P是半径OC上一动点，连结AP、PD，请求出AP＋PD的最小值，并说明理由．
（解答上面各题时，请按题意，自行补足图形）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如图①，抛物线y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点，点P在该抛物线上(P点与A、B两点不重合)．如果△ABP的三边满足AP2＋BP2＝AB2，则称点P为抛物线y＝ax2＋bx＋c(a≠0)的勾股点．
(1)直接写出抛物线y＝－x2＋1的勾股点的坐标．
(2)如图②，已知抛物线y＝ax2＋bx(a≠0)与x轴交于A，B两点，点P(1， 
)是抛物线的勾股点，求抛物线的函数表达式．
(3)在(2)的条件下，点Q在抛物线上，求满足条件S△ABQ＝S△ABP的Q点(异于点P)的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
