
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上.
上.
(1)若![]() ,
,![]() .
.
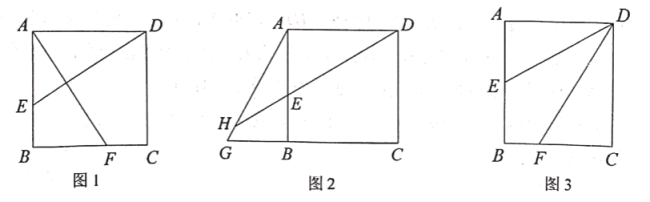
①如图1,求证:![]() ;
;
②如图2,点![]() 为
为![]() 延长线上一点,
延长线上一点,![]() 的延长线交
的延长线交![]() 于
于![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(2)如图3,若![]() 为
为![]() 的中点,
的中点,![]() .则
.则![]() 的值为 (结果用含
的值为 (结果用含![]() 的式子表示)
的式子表示)
【答案】(1)①见解析;②见解析;(2)![]()
【解析】
(1)①由“ASA”可证△ADE≌△BAF可得AE=BF;
②过点A作AF⊥HD交BC于点F,由等腰三角形的性质和平行线的性质可得∠HAF=∠AFG=∠DAF,可得AG=FG,即可得结论;
(2)过点E作EH⊥DF于H,连接EF,由角平分线的性质可得AE=EH=BE,由“HL”可证Rt△BEF≌Rt△HEF,可得BF=FH,由勾股定理可求解.
证明(1)①∵四边形ABCD是矩形,AD=AB,
∴四边形ABCD是正方形,
∴AD=AB,∠DAB=90°=∠ABC,
∴∠DAF+∠BAF=90°,
∵AF⊥DE,
∴∠DAF+∠ADE=90°,
∴∠ADE=∠BAF,且AD=AB,∠DAE=∠ABF=90°,
∴△ADE≌△BAF(ASA),
∴AE=BF;
②如图,过点A作AF⊥HD交BC于点F,
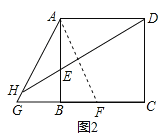
由(1)可知AE=BF,
∵AH=AD,AF⊥HD,
∴∠HAF=∠DAF.
∵AD∥BC,
∴∠DAF=∠AFG,
∴∠HAF=∠AFG,
∴AG=GF,
∴AG=GB+BF=GB+AE;
(3)如图,过点E作EH⊥DF于H,连接EF,
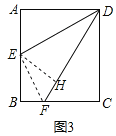
∵E为AB的中点,
∴AE=BE=![]() AB,
AB,
∵∠ADE=∠EDF,EA⊥AD,EH⊥DF,
∴AE=EH,AD=DH=nAB,
∴BE=EH,EF=EF,
∴Rt△BEF≌Rt△HEF(HL),
∴BF=FH,
设BF=x=FH,则FC=BC-BF=nAB-x,
∵DF2=FC2+CD2,
∴(nAB+x)2=(nAB-x)2+AB2,
∴x=![]() =BF,
=BF,
∴FC=![]() AB,
AB,
∴![]() =4n2-1.
=4n2-1.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知正方形ABCO,A(0,3),点D为x轴上一动点,以AD为边在AD的右侧作等腰Rt△ADE,∠ADE=90°,连接OE,则OE的最小值为( )

A. ![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
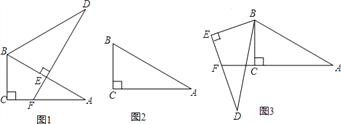
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
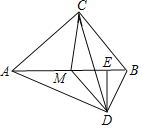
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,点M是斜边AB的中点,MD∥BC,且MD=CM,DE⊥AB于点E,连结AD、CD.
(1)求证:△MED∽△BCA;
(2)求证:△AMD≌△CMD;
(3)设△MDE的面积为S1,四边形BCMD的面积为S2,当S2=![]() S1时,求cos∠ABC的值.
S1时,求cos∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,……按此规律,则第50个图形中面积为1的正方形的个数为( )

A. 1322 B. 1323 C. 1324 D. 1325
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
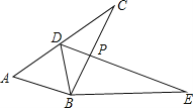
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;
(2)求△DCP与△BPE的周长和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在数学活动课中,小明剪了一张△ABC的纸片,其中∠A=60°,他将△ABC折叠压平使点A落在点B处,折痕DE,D在AB上,E在AC上.
(1)请作出折痕DE;(要求:尺规作图,不写作法,保留作图痕迹)
(2)判断△ABE的形状并说明;
(3)若AE=5,△BCE的周长为12,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来市政府每年出资新建一批廉租房,使城镇住房困难的居民住房状况得到改善.下面是某小区2006~2008年每年人口总数和人均住房面积的统计的折线图(人均住房面积=该小区住房总面积/该小区人口总数,单位:㎡/人).
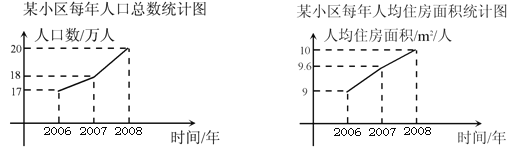
根据以上信息,则下列说法:①该小区2006~2008年这三年中,2008年住房总面积最大;②该小区2007年住房总面积达到1.728×106 m![]() ;③该小区2008年人均住房面积的增长率为4%.其中正确的有
;③该小区2008年人均住房面积的增长率为4%.其中正确的有
(A)①②③(B)①②(C)① (D)③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com