
【题目】已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为
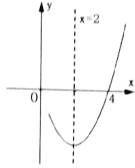
轴的一个交点坐标为![]() ,其部分图象如图所示,下列结论:①抛物线过点
,其部分图象如图所示,下列结论:①抛物线过点![]() ;②
;②![]() ;③
;③![]() ;④抛物线的顶点坐标为
;④抛物线的顶点坐标为![]() ;⑤当
;⑤当![]() 时,
时,![]() 随
随![]() 增大而增大.其中结论错误的是( )
增大而增大.其中结论错误的是( )
A.②③④B.②③⑤C.③⑤D.③④⑤
【答案】C
【解析】
①由抛物线的对称轴结合抛物线与x轴的一个交点坐标,可求出另一交点坐标,结论①正确;②由抛物线对称轴为![]() ,以及抛物线过原点,即可得出
,以及抛物线过原点,即可得出![]() 、c=0,即4a+b+c=0,结论②正确;③根据
、c=0,即4a+b+c=0,结论②正确;③根据![]() 时y<0,即可得出a+b+c<0,结论③错误;④将x=2代入二次函数解析式中,得
时y<0,即可得出a+b+c<0,结论③错误;④将x=2代入二次函数解析式中,得![]() ,结合4a+b+c=0,即可求出抛物线的顶点坐标,结论④正确;⑤观察函数图象可知,当x<2时,y随x增大而减小,结论⑤错误.综上即可得出结论.
,结合4a+b+c=0,即可求出抛物线的顶点坐标,结论④正确;⑤观察函数图象可知,当x<2时,y随x增大而减小,结论⑤错误.综上即可得出结论.
解:①∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点
标为(4,0),
∴抛物线与x轴的另一交点坐标为(0,0),结论①正确;
②∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线过原点,
∴![]() ,c=0,
,c=0,
∴![]() ,c=0,
,c=0,
∴4a+b+c=0,结论②正确;
③∵当![]() 时y<0,
时y<0,
∴a+b+c<0,结论③错误;
④当x=2时,y=ax2+bx+c=4a+2b+c=(4a+b+c)+b=b,
∴抛物线的顶点坐标为(2,b),结论④正确;
⑤观察函数图象可知:当x<2时,y随x增大而减小,结论⑤错误.
所以错误的有:③⑤;
故选择:C.


科目:初中数学 来源: 题型:
【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为( )
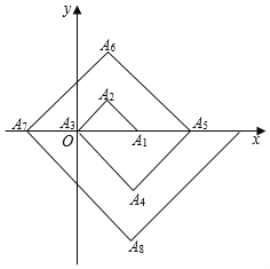
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,![]() ,E为边BC上一点,且EC=AD,连接AC.
,E为边BC上一点,且EC=AD,连接AC.
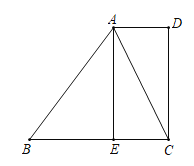
(1)求证:四边形AECD是矩形;
(2)若AC平分∠DAB,AB=5,EC=2,求AE的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长为![]() 的春游队伍,以
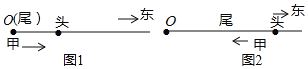
的春游队伍,以![]() 的速度向东行进,如图1和图2,当队伍排尾行进到位置
的速度向东行进,如图1和图2,当队伍排尾行进到位置![]() 时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为
时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为![]() ,当甲返回排尾后,他及队伍均停止行进.设排尾从位置
,当甲返回排尾后,他及队伍均停止行进.设排尾从位置![]() 开始行进的时间为
开始行进的时间为![]() ,排头与
,排头与![]() 的距离为
的距离为![]()
(1)当![]() 时,解答:
时,解答:
①求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围);
的取值范围);
②当甲赶到排头位置时,求![]() 的值;在甲从排头返回到排尾过程中,设甲与位置
的值;在甲从排头返回到排尾过程中,设甲与位置![]() 的距离为
的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
(2)设甲这次往返队伍的总时间为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围),并写出队伍在此过程中行进的路程.
的取值范围),并写出队伍在此过程中行进的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴正半轴交于
轴正半轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() .
.
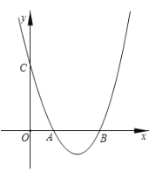
(1)若![]() 是等腰直角三角形,且其腰长为3,求抛物线的解析式;
是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(2)在(1)的条件下,点![]() 为抛物线对称轴上的一点,求
为抛物线对称轴上的一点,求![]() 的最小值
的最小值
(3)连接![]() ,在直线
,在直线![]() 下方的抛物线上,是否存在点
下方的抛物线上,是否存在点![]() ,使
,使![]() 的面积最大,若存在,请求出点
的面积最大,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
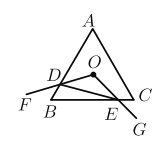
【题目】如图,等边三角形ABC的边长为4, 点O是![]() 的中心, ∠FOG = 120°, 绕点O旋转∠FOG,分别交线段AB、BC于D、 E两点,连接DE,给出下列四个结论:①OD= OE;②
的中心, ∠FOG = 120°, 绕点O旋转∠FOG,分别交线段AB、BC于D、 E两点,连接DE,给出下列四个结论:①OD= OE;②![]() ;③四边形ODBE的面积始终等于
;③四边形ODBE的面积始终等于![]() ;④
;④![]() 周长的最小值为6.上述结论中正确的有_________(写出序号)
周长的最小值为6.上述结论中正确的有_________(写出序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 ;
(2)当x 时,y随x的增大而减小;
(3)怎样移动抛物线![]() 就可以得到抛物线
就可以得到抛物线![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
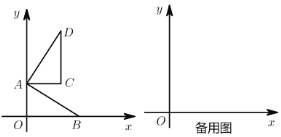
【题目】如图,在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,且
,且![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得
,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .
.
(1)点![]() 的坐标为______.
的坐标为______.
(2)解答下列问题:
①设![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ,并写出
,并写出![]() 的取值范围.
的取值范围.
②当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com