
【题目】如图所示,BC为⊙O的直径,弦AD⊥BC于E,∠C=60°. 求证:△ABD为等边三角形.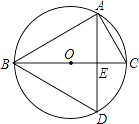
科目:初中数学 来源: 题型:
【题目】我校全体同学参加了二年级刘XX同学的捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
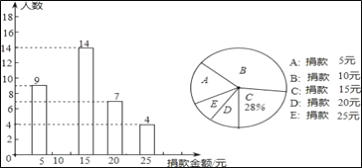
(1)本次共抽查学生 人,并将条形图补充完整;
(2)捐款金额的众数是 ,平均数是 ;
(3)在我校2200名学生中,捐款15元及以上(含15元)的学生估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴于G,连接OB,OC.
(1)判断△AOG的形状,并予以证明;
(2)若点B,C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图②,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标.
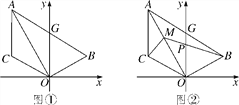
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
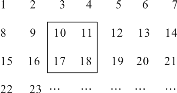
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设三角形三个内角的度数分别为x,y,z,如果其中一个角的度数是另一个角的度数的2倍,那么我们称数对(y,z)(y≤z)是x的和谐数对.例:当x=150°时,对应的和谐数对有一个,它为(10,20);当x=66时,对应的和谐数对有二个,它们为(33,81),(38,76).当对应的和谐数对(y,z)有三个时,此时x的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的根的情况( )
)x+c=0(a≠0)的根的情况( ) 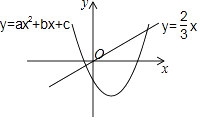
A.两根都大于0
B.两根都等于0
C.两根都小于0
D.一根大于0,一根小于0
查看答案和解析>>
科目:初中数学 来源: 题型:
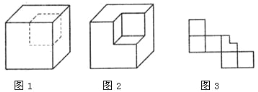
【题目】如图![]() ,大正方体上截去一个小正方体后,可得到图
,大正方体上截去一个小正方体后,可得到图![]() 的几何体.
的几何体.
![]() 设原大正方体的表面积为
设原大正方体的表面积为![]() ,图
,图![]() 中几何体的表面积为
中几何体的表面积为![]() ,那么
,那么![]() 与
与![]() 的大小关系是( )
的大小关系是( )
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、不确定
、不确定
![]() 小明说:“设图
小明说:“设图![]() 中大正方体各棱的长度之和为
中大正方体各棱的长度之和为![]() ,图
,图![]() 中几何体各棱的长度之和为
中几何体各棱的长度之和为![]() ,那么
,那么![]() 比
比![]() 正好多出大正方体
正好多出大正方体![]() 条棱的长度.”若设大正方体的棱长为
条棱的长度.”若设大正方体的棱长为![]() ,小正方体的棱长为
,小正方体的棱长为![]() ,请问
,请问![]() 为何值时,小明的说法才正确?
为何值时,小明的说法才正确?
![]() 如果截去的小正方体的棱长为大正方体棱长的一半,那么图
如果截去的小正方体的棱长为大正方体棱长的一半,那么图![]() 是图
是图![]() 中几何体的表面展开图吗?如有错误,请在图
中几何体的表面展开图吗?如有错误,请在图![]() 中修正.
中修正.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有75名工人生产A、B两种零件,一名工人每天可生产A种零件15个或B 种 零件20个,已知1个B种零件需要配3个A种零件,该车间应如何分配工人,才能保证每天生产的两种零件恰好配套?设应安排x名工人生产A种零件,根据题意,列出的方程是___________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com