
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的根的情况( )
)x+c=0(a≠0)的根的情况( ) 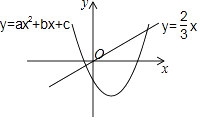
A.两根都大于0
B.两根都等于0
C.两根都小于0
D.一根大于0,一根小于0
【答案】D
【解析】解:设ax2+bx+c=0(a≠0)的两根为x1 , x2 , ∵由二次函数的图象可知x1x2<0,
∴ ![]() <0.
<0.
设方程ax2+(b﹣ ![]() )x+c=0(a≠0)的两根为m,n,则mn=
)x+c=0(a≠0)的两根为m,n,则mn= ![]() <0,
<0,
∴方程ax2+(b﹣ ![]() )x+c=0(a≠0)的两根为一根大于0,一根小于0,
)x+c=0(a≠0)的两根为一根大于0,一根小于0,
故选D.
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】保护环境、低碳出行已渐渐成为人们的习惯.最近无为县城又引进了共享单车,只需要交点押金,就可以通过扫描二维码的方式解锁一辆停在路边的自行车,以极低的费用,轻松骑到目的地.王老师家与学校相距2km,现在每天骑共享单车到学校所花的时间比过去骑电动车多用4min.已知王老师骑电动车的速度是骑共享单车速度的1.5倍,则王老师骑共享单车的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,记△=b2﹣4ac,M=(2ax1+b)2 , 则关于△与M大小关系的下列说法中,正确的是( )
A.△>M
B.△=M
C.△<M
D.无法确定△与M的大小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地. 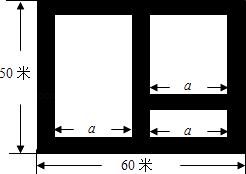
(1)设通道的宽度为x米,则a=(用含x的代数式表示);
(2)若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1: ![]() ,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= .
,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= . 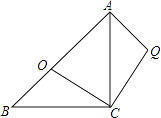
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道1+2+3+…+![]() =
=![]() ,则1+2+3+…+10= ___________ .
,则1+2+3+…+10= ___________ .
[问题提出] 那么 ![]() 的结果等于多少呢?
的结果等于多少呢?
[阅读理解] 在图1所示的三角形数阵中,第1行圆圈中的数为1,即12 ;第2行两个圆圈中数的和为2+2,即22;......;第n行n个圆圈中数的和为n+n+![]() n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
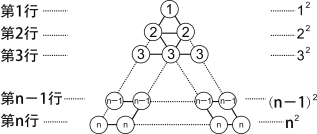
图1
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n-1行的第一个圆圈中的数分别为n-1,2,n)发现每个位置上三个圆圈中的数的和均为______________.由此可得,这三个三角形数阵所有圆圈中数的总和为:
3(![]() )=_________________.因此,
)=_________________.因此,![]() =__________.
=__________.
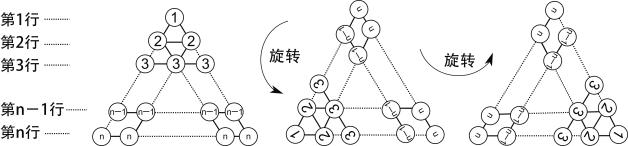
图2
[问题解决]
(1).根据以上规律可得![]() __________________.
__________________.
(2).试计算 ![]() ,请写出计算步骤.
,请写出计算步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
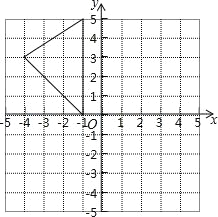
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
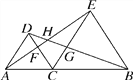
【题目】如图,在线段AB上取一点C(非中点),分别以AC、BC为边在AB的同侧作等边△ACD和等边△BCE,连接AE交CD于F,连接BD交CE于G,AE和BD交于点H,则下列结论:①AE=DB;②不另外添加线,图中全等三角形只有1对;③若连接FG,则△CFG是等边三角形;④若连接CH,则CH平分∠FHG.其中正确的是________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com