
【题目】已知x1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,记△=b2﹣4ac,M=(2ax1+b)2 , 则关于△与M大小关系的下列说法中,正确的是( )
A.△>M
B.△=M
C.△<M
D.无法确定△与M的大小
科目:初中数学 来源: 题型:
【题目】解方程:
(1) 5(x+8)=6(2x-7)+5;
(2) 5-![]() =x;
=x;
(3) ![]() -
-![]() =1;
=1;
(4) ![]() -
-![]() =1;
=1;
(5) 2x-![]() [x-
[x-![]() (x-1)]=
(x-1)]=![]() ( x-1).
( x-1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售“喜羊羊”玩具,预测该产品能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,商场又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了10元.
(1)该商场两次共购进这种玩具多少个?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每件售价至少是多少元?(利润率![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
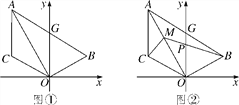
【题目】如图①,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴于G,连接OB,OC.
(1)判断△AOG的形状,并予以证明;
(2)若点B,C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图②,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( ) 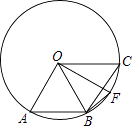
A.12.5°
B.15°
C.20°
D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
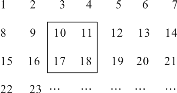
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设三角形三个内角的度数分别为x,y,z,如果其中一个角的度数是另一个角的度数的2倍,那么我们称数对(y,z)(y≤z)是x的和谐数对.例:当x=150°时,对应的和谐数对有一个,它为(10,20);当x=66时,对应的和谐数对有二个,它们为(33,81),(38,76).当对应的和谐数对(y,z)有三个时,此时x的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y= ![]() x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣ ![]() )x+c=0(a≠0)的根的情况( )
)x+c=0(a≠0)的根的情况( ) 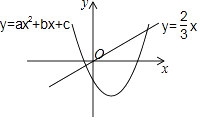
A.两根都大于0
B.两根都等于0
C.两根都小于0
D.一根大于0,一根小于0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() 平分
平分![]() ,即
,即![]() ,
,![]() 平分
平分![]() ,即
,即![]() ;
;
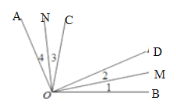
![]() 若
若![]() ,则
,则![]() ________;
________;
![]() 若
若![]() 可以在
可以在![]() 内部绕点
内部绕点![]() 作任意旋转(射线
作任意旋转(射线![]() 与射线
与射线![]() 不重合,射线
不重合,射线![]() 与射线
与射线![]() 不重合)则
不重合)则![]() 的大小是否改变?试说明理由.
的大小是否改变?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com