
【题目】阅读下列材料,并解爷其后的问题:
我们知道,三角形的中位线平行于第一边,且等于第三边的一半,我们还知道,三角形的三条中位线可以将三角形分成四个全等的一角形,如图1,若D、E、F分别是![]() 三边的中点,则有
三边的中点,则有![]() ,且
,且![]()



(1)在图1中,若![]() 的面积为15,则
的面积为15,则![]() 的面积为___________;
的面积为___________;
(2)在图2中,已知E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边形EFGH是平行四边形;
(3)如图3中,已知E、F、G、H分别是AB、BC、CD、AD的中点,![]() ,则四边形EFGH的面积为___________.
,则四边形EFGH的面积为___________.
【答案】(1)![]() ;(2)见解析;(3)5.
;(2)见解析;(3)5.
【解析】
(1)由三角形中位线定理得出DF∥BC,且DF=![]() BC,△ADF≌△DBE≌△FEC≌△EFD,得出△DEF的面积=
BC,△ADF≌△DBE≌△FEC≌△EFD,得出△DEF的面积=![]() △ABC的面积=
△ABC的面积=![]() 即可;
即可;
(2)连接BD,证出EH是△ABD的中位线,FG是△BCD的中位线,由三角形中位线定理得出EH∥BD,EH=![]() BD,FG∥BD,FG=
BD,FG∥BD,FG=![]() BD,得出EH∥FG,EH=FG,即可得出结论;
BD,得出EH∥FG,EH=FG,即可得出结论;
(3)证出EH是△ABD的中位线,FG是△BCD的中位线,由三角形中位线定理得出EH∥BD,EH=![]() BD=
BD=![]() ,FG∥BD,FG=
,FG∥BD,FG=![]() BD,得出EH∥FG,EH=FG,证出四边形EFGH是平行四边形,同理:EF∥AC,EF=
BD,得出EH∥FG,EH=FG,证出四边形EFGH是平行四边形,同理:EF∥AC,EF=![]() AC=2,证出EH⊥EF,得出四边形EFGH是矩形,即可得出结果.
AC=2,证出EH⊥EF,得出四边形EFGH是矩形,即可得出结果.
(1)解:∵D、E、F分别是△ABC三边的中点,
则有DF∥BC,且DF=![]() BC,△ADF≌△DBE≌△FEC≌△EFD,
BC,△ADF≌△DBE≌△FEC≌△EFD,
∴△DEF的面积=![]() △ABC的面积=
△ABC的面积=![]() ;
;
故答案为:![]() ;
;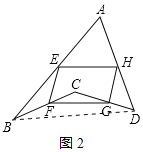
(2)证明:连接BD,如图2所示:
∵E、F、G、H分别是AB、BC、CD、AD的中点,
∴EH是△ABD的中位线,FG是△BCD的中位线,
∴EH∥BD,EH=![]() BD,FG∥BD,FG=
BD,FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
(3)解:∵E、F、G、H分别是AB、BC、CD、AD的中点,
∴EH是△ABD的中位线,FG是△BCD的中位线,
∴EH∥BD,EH=![]() BD=
BD=![]() ,FG∥BD,FG=
,FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形,
同理:EF∥AC,EF=![]() AC=2,
AC=2,
∵AC⊥BD,
∴EH⊥EF,
∴四边形EFGH是矩形,
∴四边形EFGH的面积=EH×EF=![]() ×2=5.
×2=5.
故答案为:(1)![]() ;(2)见解析;(3)5.
;(2)见解析;(3)5.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
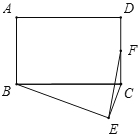
A. 8B. 9C. 10D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且![]() .
.
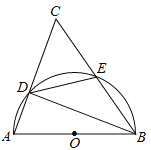
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中描出下列各组点,并将各组的点用线段依次连结起来.
(1)(1,0)、(6,0)、(6,1)、(5,0)、(6,-1)、(6,0);
(2)(2,0)、(5,3)、(4,0);
(3)(2,0)、(5,-3)、(4,0).
观察所得到的图形像什么?如果要将此图形向上平移到x轴上方,那么至少要向上平移几个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某九年级制学校围绕“每天30分钟的大课间,你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:

(1)该校对多少学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方体敞口玻璃罐,长、宽、高分别为16 cm、6 cm和6 cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2 cm处,则蚂蚁到达饼干的最短距离是多少cm.( )
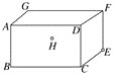
A. 7![]() B.
B. ![]()
C. 24D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市“健益”超市购进一批![]() 元/千克的绿色食品,如果以
元/千克的绿色食品,如果以![]() 元/千克销售,那么每天可售出
元/千克销售,那么每天可售出![]() 千克.由销售经验知,每天销售量
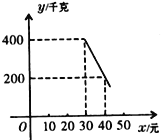
千克.由销售经验知,每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)(
(元)(![]() )存在如下图所示的一次函数关系.
)存在如下图所示的一次函数关系.
(1)试求出y与x的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润p元,当销售单价为何值时,每天可获得 最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过4480元,现该超市经理要求每天利润不得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com