
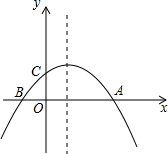
 如图,已知抛物线y=-$\frac{1}{a}$(x+2)(x-a)(a>0)与x轴交于点A,B(点A在点B右侧),与y轴交于点C,抛物线过点N(6,一4).
如图,已知抛物线y=-$\frac{1}{a}$(x+2)(x-a)(a>0)与x轴交于点A,B(点A在点B右侧),与y轴交于点C,抛物线过点N(6,一4).分析 (1)将N点坐标代入即可求得;
(2)由于A、B关于对称轴对称,所以相当于求AH+CH的最小值,根据两点之间线段最短,当A、H、C三点共线时AH+CH最小,即连接AC与对称轴的交点就是H,求出AC解析式,再与对称轴方程联立即可求得;
(3)分两种情况:①作BF∥AC交抛物线于点F,先求出BF解析式,再与抛物线方程联立求出F点坐标,再用两点间的距离公式表示出BF的长度,接着利用相似比例关系列出方程求解;②在x轴下方作∠ABF=∠ABC=45°,同样先求出BF解析式,再求出F点坐标,进而表示出BF长度,最后利用相似比例关系列方程求解.算的过程中,可能有一种情况无解,舍去就是了.
解答 解:(1)∵抛物线y=-$\frac{1}{a}$(x+2)(x-a)(a>0)过点N(6,一4),
∴-4=$-\frac{1}{a}(6+2)(6-a)$,
解得,a=4,
即实数a的值为4;
(2)∵a=4
∴$y=-\frac{1}{4}(x+2)(x-4)$
令y=0,得x1=-2,x2=4;令x=0,得y=2
∴点A的坐标为(4,0),点B的坐标为(-2,0),点C的坐标为(0,2)
∵点A和点B关于抛物线的对称轴x=$\frac{-2+4}{2}=1$对称,
∴在抛物线的对称轴上找一点H,使得BH+CH最小,即AH+CH最小,连接AC,则AC与抛物线的对称轴x=1的交点即为所求
如下图所示: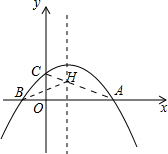
设过点A(4,0),C(0,2)的直线解析式为:y=kx+b
则$\left\{\begin{array}{l}{0=k×4+b}\\{2=k×0+b}\end{array}\right.$
解得k=$-\frac{1}{2}$,b=2
∴y=$-\frac{1}{2}x+2$
令x=1代入y=$-\frac{1}{2}x+2$,得y=$\frac{3}{2}$
∴点H的坐标为(1,$\frac{3}{2}$)
即点H的坐标为(1,$\frac{3}{2}$)时,使得BH+CH最小;
(3)①作BF∥AC交抛物线于点F,如图: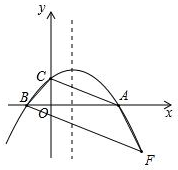
则∠FBA=∠BAC,
由y=-$\frac{1}{a}$(x+2)(x-a)=-$\frac{1}{a}{x}^{2}+(1-\frac{2}{a})x+2$,
令x=0,则y=2,
∴C(0,2),
又∵A(a,0),
∴AC的解析式为y=$-\frac{2}{a}x+2$,
设BF的解析式为y=$-\frac{2}{a}x+b$,
∵BF过点B(-2,0),
∴b=$-\frac{4}{a}$,
∴BF的解析式为:y=$-\frac{2}{a}x-\frac{4}{a}$,
∴$\left\{\begin{array}{l}{y=-\frac{2}{a}x-\frac{4}{a}}\\{y=-\frac{1}{a}{x}^{2}+(1-\frac{2}{a})x+2}\end{array}\right.$,
解得:F(a+2,-2-$\frac{8}{a}$),
∴BF=$\sqrt{(a+4)^{2}+(2+\frac{8}{a})^{2}}$
∵△BFA∽△ABC,
∴AB2=BF•AC,
∴$(a+2)^{2}=\sqrt{{(a+4)}^{2}+{(2+\frac{8}{a})}^{2}}•\sqrt{{a}^{2}+4}$,
化简整理得:16=0,不存在这种情形,
即这种情况不存满足要求的F点;
②∵B(-2,0),C(2,0),
∴BC的解析式为y=x+2,∠ABC=45°,
在x轴下方作∠ABF=∠ABC=45°,如图: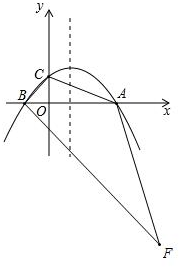
∴BF⊥BC,
∴BF的解析式为y=-x-2,
∴$\left\{\begin{array}{l}{y=-x-2}\\{y=-\frac{1}{a}{x}^{2}+(1-\frac{2}{a})x+2}\end{array}\right.$,
解得:F(2a,-2a-2),
∴BF=$\sqrt{(2a+2)^{2}+(2a+2)^{2}}$,
∵△BFA∽△BAC,
∴AB2=BF•BC,
∴${(a+2)}^{2}=\sqrt{{(2a+2)}^{2}+{(2a+2)}^{2}}•2\sqrt{2}$,
整理得:a2-4a-4=0,
解得a=$2+2\sqrt{2}$或a=$2-2\sqrt{2}$(舍去),
综上所述,a=$2+2\sqrt{2}$时,以点B,A,F为顶点的三角形与△BAC相似.
点评 考查了二次函数综合题,解决二次函数问题应注意对称性的应用,若已知三点坐标,可设一般式;若已知顶点坐标,可设顶点式;若已知抛物线与x轴两交点坐标,可设两点式,从而简化运算,整个问题围绕二次函数展开,并将二次函数、三角形等多个问题紧密地结合在一起,无论是题设的给出还是思维方式的考查都很新颖.一道考题不仅考查了二次函数、三角形相似等初中数学中的重点内容,还考查了待定系数法等数学思想方法,这是中考试卷的创新题型和发展趋势,代数知识与几何知识得到了很好的整合,是一个典型的在知识网络交汇点处设计的热点试题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在等边△ABC中,点D,E分別在边BC,AC上,DE∥AB,过点E作EF丄DE,交BC的延长线于点F.
如图,在等边△ABC中,点D,E分別在边BC,AC上,DE∥AB,过点E作EF丄DE,交BC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
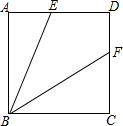 已知:如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于F,若正方形边长为2$\sqrt{5}$,AE=4,求DF的长.
已知:如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于F,若正方形边长为2$\sqrt{5}$,AE=4,求DF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
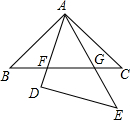 如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.
如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 只有1,-7,+101,-9是整数 | B. | 其中有三个数是正整数 | ||
| C. | 非负数有1,8.6,0,$\frac{5}{6}$,+101 | D. | 只有-$\frac{4}{5}$,-4$\frac{2}{3}$是负分数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
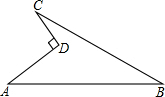 如图所示的一块地,其中∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,
如图所示的一块地,其中∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com