
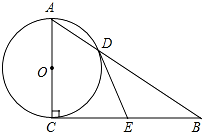
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线DE,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D的切线DE,交BC于E.分析 (1)连接OD、CD,结合AC为直径可得到∠CDB=90°,由ED=CE,再利用角的和差可求得∠ODE=90°,然后根据同角的余角相等证得∠EDB=∠B,由等腰三角形的判定即可得到结论;
(2)证明∠B=45°,∠A=45°,进而证明AC=BC即可解决问题.
解答 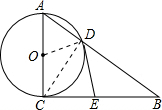 (1)证明:如图,连接OD、CD,
(1)证明:如图,连接OD、CD,
∵OC=OD,
∴∠OCD=∠ODC,
∵AC为⊙O的直径,
∴∠CDB=90°,
∵E为BC的中点,
∴DE=CE,
∴∠ECD=∠EDC,
∴∠OCD+∠ECD=∠ODC+∠EDC=90°,
∴∠ODE=∠ACB=90°,
即OD⊥DE,
∴∠ODC+∠CDE=∠OCD+DCE=90°,
∵OC=OD,∴∠OCD=∠ODC,
∴∠DCE=∠CDE,
同理∠EDB=∠B,
∴DE=BE;
(2)解:△ABC是等腰直角三角形,
当以点O、D、E、C为顶点的四边形是正方形时,则∠DEB=90°,
又∵DE=BE,
∴△DEB是等腰直角三角形,
则∠B=45°,∠A=45°,
∴AC=BC,
∴△ABC是等腰直角三角形.
点评 本题主要考查切线的判定及等腰直角三角形的判定,掌握切线的判定方法是解题的关键.


科目:初中数学 来源: 题型:填空题
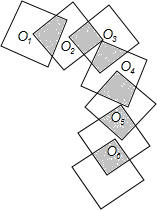 如图,7个正方形的边长均为1,O1、O2、O3、O4、O5、O6是前面六个正方形的中心,同时又是后面六个正方形的顶点,则图中阴影部分的面积是1.5.
如图,7个正方形的边长均为1,O1、O2、O3、O4、O5、O6是前面六个正方形的中心,同时又是后面六个正方形的顶点,则图中阴影部分的面积是1.5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
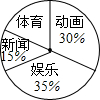 某校调查了九年级820名学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况,绘制成所示的扇形统计图,则该校喜爱体育节目的学生有164名.
某校调查了九年级820名学生对新闻、体育、动画、娱乐四类电视节目的喜爱情况,绘制成所示的扇形统计图,则该校喜爱体育节目的学生有164名.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
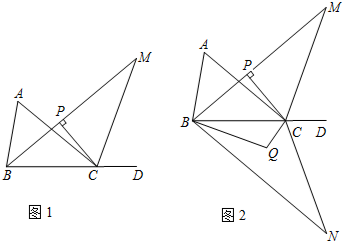
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:选择题
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
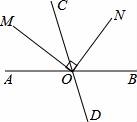
A.35° B.45° C.55° D.65°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com