
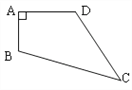
【题目】已知,如图9,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积____________.
【答案】36(cm2).
【解析】首先连接BD,再利用勾股定理计算出BD的长,再根据勾股定理逆定理计算出∠D=90°,然后计算出直角三角形ABD和直角三角形BDC的面积,即可算出答案.
解:连接BD,

∵∠A=90°,AB=3cm,AD=4cm,
∴BD=![]() =
=![]() =5(cm),
=5(cm),
∵52+122=132,
∴BD2+CD2=CB2,
∴∠BDC=90°,
∴S△DBC=![]() ×DB×CD=
×DB×CD=![]() ×5×12=30(cm2),
×5×12=30(cm2),
S△ABD=![]() ×3×4=6(cm2),
×3×4=6(cm2),
∴四边形ABCD的面积为30+6=36(cm2),
故答案为:36(cm2).
“点睛”此题主要考查了勾股定理,以及勾股定理的逆定理,解决此题的关键是算出BD的长,△BDC是直角三角形.


科目:初中数学 来源: 题型:
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=﹣2x+2的图象.

(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
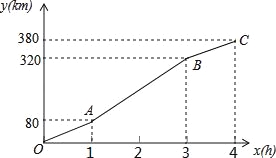
【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县区大力发展甜瓜产业,预计今年A地将采摘200吨,B地将采摘300吨.若要将这些甜瓜运到甲、乙两个冷藏仓库,已知甲仓库可储存240吨,乙仓库可储存260吨,从A地运往甲、乙两处的费用分别为每吨20元和25元,从B地运往甲、乙两处的费用分别为每吨15元和18元.设从A地运往甲仓库的甜瓜为x吨,A、B两地运往两仓库的甜瓜运输费用分别为![]() .
.
(1)分别求出![]() 与x之间的函数关系式;
与x之间的函数关系式;
(2)试讨论A、B两地中,哪个的运费较少;
(3)考虑B地的经济承受能力,B地的甜瓜运费不得超过4830元,在这种情况下,请问怎样调运才能使两地运费之和最少?求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016浙江省温州市第22题)有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
甲种糖果 | 乙种糖果 | 丙种糖果 | |
单价(元/千克) | 15 | 25 | 30 |
千克数 | 40 | 40 | 20 |
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com