
(11分)如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
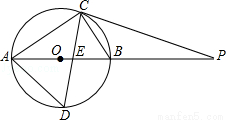
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
(1)AC=8,AD=5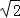 cm;(2)直线PC与⊙O相切,理由见解析.
cm;(2)直线PC与⊙O相切,理由见解析.
【解析】
试题分析:(1)连接BD,在RT△ABC中,由勾股定理可得AC=8,在等腰直角三角形ABD中可得AD=5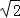 cm;
cm;
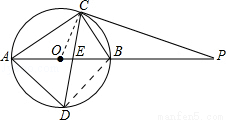
(2)观察图形可得直线PC与⊙O相切,连接OC,根据条件证明OC⊥PC,即可.
试题解析:【解析】
(1)①如图,连接BD,
∵AB是直径,
∴∠ACB=∠ADB=90°,
在RT△ABC中,
AC= =
=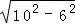 =8, 3分
=8, 3分
②∵CD平分∠ACB,
∴AD=BD,
∴Rt△ABD是等腰直角三角形,
∴AD=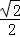 AB=
AB=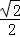 ×10=5
×10=5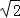 cm; 6分
cm; 6分
(2)直线PC与⊙O相切,
理由:连接OC,
∵OC=OA,
∴∠CAO=∠OCA,
∵PC=PE,
∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE,
∵CD平分∠ACB,
∴∠ACE=∠ECB,
∴∠PCB=∠ACO,
∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°,
OC⊥PC,
∴直线PC与⊙O相切. 11分
考点:1.圆周角定理及其推论;2.勾股定理;3.等腰直角三角形的判定与性质;4.切线的判定.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(﹣2,4),B(﹣2,1),C(﹣5,2).
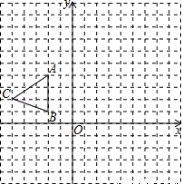
(1)请画出△ABC关于x轴对称的△A1B1C1.
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以﹣2,得到对应的点A2,B2,C2,请画出△A2B2C2.
(3)求△A1B1C1与△A2B2C2的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于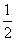 AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
AC长为半径画弧,两弧相交于点M、N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
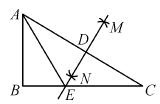
(1)∠ADE= ;
(2)AE CE(填“>”“<”或“=”)
(3)AB=3,AC=5时,△ABE的周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
平面内的两条直线有相交和平行两种位置关系.

(1)如图1,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图2,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)在图2中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省长汀县城区三校九年级12月联考数学试卷(解析版) 题型:解答题
(每小题6分共12分)解方程
(1)2(x+2)2-8=0 ;
(2)2x2-7x+3=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,若点C也在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C个数是( )
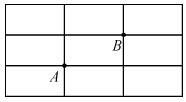
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省七年级上学期期末调研数学试卷(解析版) 题型:填空题
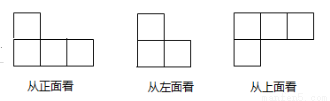
一个由小立方块搭成的几何体,从正面、左面、上面看到的形状图如图所示, 这个几何体是由 个小立方块搭成的 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com