
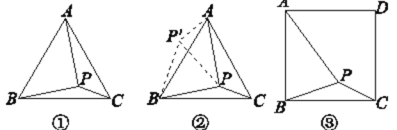
【题目】问题:如图①,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC的度数和等边三角形ABC的边长.
,PC=1,求∠BPC的度数和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图②),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),可得∠AP′B= °,所以∠BPC=∠AP′B= °,还可证得△ABP是直角三角形,进而求出等边三角形ABC的边长为 ,问题得到解决.
(1)根据李明同学的思路填空:∠AP′B= °,∠BPC=∠AP′B= °,等边三角形ABC的边长为 .
(2)探究并解决下列问题:如图③,在正方形ABCD内有一点P,且PA=![]() ,PB=
,PB=![]() ,PC=1.求∠BPC的度数和正方形ABCD的边长.
,PC=1.求∠BPC的度数和正方形ABCD的边长.
【答案】(1)∠AP′B=150°,∠BPC=∠AP′B=150°,等边三角形ABC的边长为![]() ;(2)∠BPC=135°,正方形ABCD的边长为
;(2)∠BPC=135°,正方形ABCD的边长为![]() .
.
【解析】
根据旋转得出AP′=CP=1,BP′=BP=![]() ,∠PBC=∠P′BA,∠AP′B=∠BPC,求出∠ABP′+∠ABP=60°,得到等边△BPP′,推出PP′=
,∠PBC=∠P′BA,∠AP′B=∠BPC,求出∠ABP′+∠ABP=60°,得到等边△BPP′,推出PP′=![]() ,∠BP′P=60°,求出∠AP′P=90°即可求出∠BPC;过点B作BM⊥AP′,交AP′的延长线于点M,由∠MP′B=30°,求出BM=
,∠BP′P=60°,求出∠AP′P=90°即可求出∠BPC;过点B作BM⊥AP′,交AP′的延长线于点M,由∠MP′B=30°,求出BM=![]() ,P′M=
,P′M=![]() ,根据勾股定理即可求出答案;
,根据勾股定理即可求出答案;
(2)求出∠BEP=![]() (180°-90°)=45°,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;过点B作BF⊥AE,交AE的延长线于点F,求出FE=BF=1,AF=2,关键勾股定理即可求出AB.
(180°-90°)=45°,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;过点B作BF⊥AE,交AE的延长线于点F,求出FE=BF=1,AF=2,关键勾股定理即可求出AB.
(1)∵等边△ABC,
∴∠ABC=60°,
将△BPC绕点B逆时针旋转60°得出△ABP′,
∴AP′=CP=1,BP′=BP=![]() ,∠PBC=∠P′BA,∠AP′B=∠BPC,
,∠PBC=∠P′BA,∠AP′B=∠BPC,
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP′+∠ABP=∠ABC=60°,
∴△BPP′是等边三角形,
∴PP′=![]() ,∠BP′P=60°,
,∠BP′P=60°,
∵AP′=1,AP=2,
∴AP′2+PP′2=AP2,
∴∠AP′P=90°,
∴∠BPC=∠AP′B=90°+60°=150°,
过点B作BM⊥AP′,交AP′的延长线于点M,
∴∠MP′B=30°,BM=![]() ,
,
由勾股定理得:P′M=![]() ,
,
∴AM=1+![]() =
=![]() ,
,
由勾股定理得:AB=![]() ,
,
故答案为:150°,![]() .
.
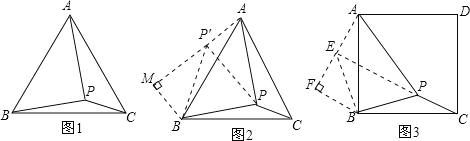
(2)将△BPC绕点B逆时针旋转90°得到△AEB,
与(1)类似:可得:AE=PC=1,BE=BP=![]() ,∠BPC=∠AEB,∠ABE=∠PBC,
,∠BPC=∠AEB,∠ABE=∠PBC,
∴∠EBP=∠EBA+∠ABP=∠ABC=90°,
∴∠BEP=![]() (180°-90°)=45°,
(180°-90°)=45°,
由勾股定理得:EP=2,
∵AE=1,AP=![]() ,EP=2,
,EP=2,
∴AE2+PE2=AP2,
∴∠AEP=90°,
∴∠BPC=∠AEB=90°+45°=135°,
过点B作BF⊥AE,交AE的延长线于点F;
∴∠FEB=45°,
∴FE=BF=1,
∴AF=2;
∴在Rt△ABF中,由勾股定理,得AB=![]() ;
;
∴∠BPC=135°,正方形边长为![]() .
.
答:∠BPC的度数是135°,正方形ABCD的边长是![]() .
.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=2x2+bx+c.当x=1时,y=4;当x=﹣2,y=﹣5.
(1)求y关于x的二次函数的解析式;
(2)在直角坐标系中把(1)中的图象抛物线平移到顶点与原点重合,应该怎样平移?
查看答案和解析>>
科目:初中数学 来源: 题型:
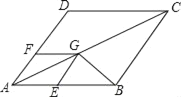
【题目】如图,四边形ABCD和AEGF都是菱形,∠A=60°,AD=3,点E,F分别在AB,AD边上(不与端点重合),当△GBC为等腰三角形时,AF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
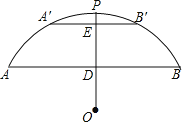
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
查看答案和解析>>
科目:初中数学 来源: 题型:
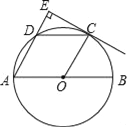
【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为(2a+3b),宽为(a+b)的大长方形,则需要A类、B类和C类卡片的张数分别为( )
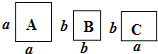
A.3,5,2B.3,7,2C.2,3,5D.2,5,7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com