
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬������y=ax2+2xa+c����A����4��0����B��0��4�����㣬��x�ύ����һ��C��ֱ��y=x+5��x�ύ�ڵ�D����y�ύ�ڵ�E��
��1���������ߵĽ���ʽ��
��2����P�ǵڶ������������ϵ�һ�����㣬����EP������E��EP�Ĵ���l����l�Ͻ�ȡ�߶�EF��ʹEF=EP���ҵ�F�ڵ�һ���ޣ�����F��FM��x���ڵ�M�����P�ĺ�����Ϊt���߶�FM�ij���Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ����
��3���ڣ�2���������£�����E��EH��ED��MF���ӳ����ڵ�H������DH����GΪDH���е㣬��ֱ��PG����AC���е�Qʱ�����F�����꣮
���𰸡�
��1��
�⣺��A����4��0����B��0��4������y=ax2+2xa+c�� ![]() �����
����� 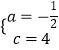 ��
��
���������߽���ʽΪy=�� ![]() x2��x+4
x2��x+4
��2��
�⣺��ͼ1���ֱ��P��F��y�������ߣ�����ֱ�ΪA�䡢B�䣬��P��PN��x�ᣬ����ΪN��

��ֱ��DE�Ľ���ʽΪ��y=x+5����E��0��5����
��OE=5��
�ߡ�PEO+��OEF=90�㣬��PEO+��EPA��=90�㣬
���EPA��=��OEF��
��PE=EF����EA��P=��EB��F=90�㣬
���PEA��ա�EFB�䣬
��PA��=EB��=��t��
��d=FM=OB��=OE��EB��=5������t��=5+t
��3��
�⣺��ͼ2����ֱ��DE�Ľ���ʽΪ��y=x+5��
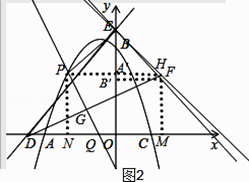
��EH��ED��
��ֱ��EH�Ľ���ʽΪ��y=��x+5��
��FB��=A��E=5������ ![]() t2��t+4��=
t2��t+4��= ![]() t2+t+1��
t2+t+1��
��F�� ![]() t2+t+1��5+t����
t2+t+1��5+t����
���H�ĺ�����Ϊ�� ![]() t2+t+1��
t2+t+1��
y=�� ![]() t2��t��1+5=��
t2��t��1+5=�� ![]() t2��t+4��
t2��t+4��
��H�� ![]() t2+t+1����
t2+t+1���� ![]() t2��t+4����
t2��t+4����
����PH��y����A�䣬
��P��H����������ȣ�
��PH��x�ᣬ
���HPQ=��PQD����PGH=��QGD��
��DG=GH��
���PGH�ա�QGD��
��PH=DQ��
��A����4��0����C��2��0����
��Q����1��0����
��D����5��0����
��DQ=PH=4��
�ੁt+ ![]() t2+t+1=4��
t2+t+1=4��
t=�� ![]() ��
��
��P�ڵڶ����ޣ�
��t��0��
��t=�� ![]() ��
��
��F��4�� ![]() ��5��
��5�� ![]() ����
����
����������1�����ô���ϵ��������κ����Ľ���ʽ����2����ͼ1���������߹�������ֱ�������Σ�����б��PE=EF���������֤��ֱ��������ȫ�ȣ���PA��=EB�䣬��d=FM=OE��EB�������ʽ�ɵý��ۣ���Ҫע��PA��=��t����3����ͼ2������ֱ��EH�Ľ���ʽ��ʾ����F�������H�����꣬���ֵ�P�͵�H����������ȣ���PH��x��ƽ�У�֤����PGH�ա�QGD����PH=DQ=4����ʽ�ɵ�t��ֵ�����t��ֵ��ȡ�ᣬ�������F�����꣮Ҳ���������߶��е㹫ʽ������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�MN��3cm�����߶�MN��ȡһ��P��ʹPM��PN���ӳ��߶�MN����A��ʹAN��![]() MN���ӳ��߶�NM����B��ʹBN��3BM.
MN���ӳ��߶�NM����B��ʹBN��3BM.
(1)�������⣬����ͼ�Σ�
(2)���߶�AB�ij���
(3)��˵����P����Щ�߶ε��е�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ�飺 ![]() ������������գ���ɱ���Ľⷨ��
������������գ���ɱ���Ľⷨ�� ![]()
��1���ⲻ��ʽ��1��������
��2���ⲻ��ʽ��2��������
��3���Ѳ���ʽ ��1���� ��2���Ľ⼯�������ϱ�ʾ������
��4��ԭ����ʽ�Ľ⼯Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���۵�����ABCD��һ��AD��ʹ��D����BC�ߵĵ�F������֪�ۺ�AE=5 ![]() cm����tan��EFC=
cm����tan��EFC= ![]() �������ABCD���ܳ��� ��
�������ABCD���ܳ��� �� 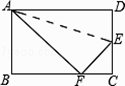
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90������B=30������AΪԲ�ģ����ⳤΪ�뾶�����ֱ�AB��AC�ڵ�M��N���ٷֱ���M��NΪԲ�ģ�����MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D��������˵������ȷ�ĸ�����
��AD����BAC��ƽ���ߣ��ڡ�ADC=60��������D��AB���д����ϣ���S��DAC��S��ABC=1��3��

A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ֽ���ʽ��![]() ��2���ֽ���ʽ�� 9a2��x��y��+4b2��y��x��
��2���ֽ���ʽ�� 9a2��x��y��+4b2��y��x��
��3���ֽ���ʽ��(x2��y2)2��4x2y2 ��4�����÷ֽ���ʽ������ֵ��2662-2342
��5�����÷ֽ���ʽ������ֵ����֪x-3y=-1��xy=2����x3y-6x2y2+9xy3��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y= ![]() x+2��˫����y=
x+2��˫����y= ![]() �ཻ�ڵ�A��m��3������x�ύ�ڵ�C��
�ཻ�ڵ�A��m��3������x�ύ�ڵ�C�� 
��1����˫���߽���ʽ��
��2����P��x���ϣ������ACP�����Ϊ3�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݹ��ҷ���ίʵʩ�����ݵ�������й��ļ�Ҫ�������н�ϵط�ʵ�ʣ������Ծ��������õ����������ݵ�����շѣ������շѱ�������
һ������һ�����õ����ķ�Χ | ��Ѽ۸�λ��Ԫ/ǧ��ʱ�� |
������150ǧ��ʱ | a |
����150ǧ��ʱ�IJ��� | b |
2017��5�·ݣ�������õ�100�ȣ������80Ԫ���������õ�190�ȣ������160Ԫ��
��1������a=�� ����b=�� ����
��2�����������ݵ�����շ��Ժ���һ������2017��8�·�ƽ�����ÿ��Ϊ0.9Ԫ������û�8���õ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=x2+bx+3��ͼ����x�������ύ��B��C���㣬BC=2����b��ֵΪ�� ��

A��4 B����4 C����4 D����5
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com