练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知线段MN＝3cm，在线段MN上取一点P，使PM＝PN；延长线段MN到点A，使AN＝MN；延长线段NM到点B，使BN＝3BM.

    (1)根据题意，画出图形；

    (2)求线段AB的长；

    (3)试说明点P是哪些线段的中点.

    【答案】（1）作图见解析；（2）1.5cm；（3）理由见解析.

    【解析】

    整体

    根据题意，判断出BM=MP=PN=NA，即可求解.

    (1)如图所示．

    (2)因为MN＝3cm，AN＝MN，所以AN＝1.5cm.

    因为PM＝PN，BN＝3BM，所以BM＝PM＝PN，

    所以BM＝MN＝×3＝1.5(cm)

    所以AB＝BM＋MN＋AN＝1.5＋3＋1.5＝6(cm)

    (3)由(2)可知BM＝MP＝PN＝NA

    所以PB＝PA，PM＝PN

    所以点P既是线段MN的中点，也是线段AB的中点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】顾琪在学习了《展开与折叠》这一课后，明白了很多几何体都能展开成平面图形．于是她在家用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的①和②．根据你所学的知识，回答下列问题：

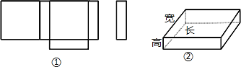
    顾琪总共剪开了________条棱．

    现在顾琪想将剪断的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为她应该将剪断的纸条粘贴到①中的什么位置？请你帮助她在①上补全．

    已知顾琪剪下的长方体的长、宽、高分别是、、，求这个长方体纸盒的体积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在社会主义新农村建设中，衢州某乡镇决定对A、B两村之间的公路进行改造，并有甲工程队从A村向B村方向修筑，乙工程队从B村向A村方向修筑．已知甲工程队先施工3天，乙工程队再开始施工．乙工程队施工几天后因另有任务提前离开，余下的任务有甲工程队单独完成，直到公路修通．下图是甲乙两个工程队修公路的长度y（米）与施工时间x（天）之间的函数图象，请根据图象所提供的信息解答下列问题：

    （1）乙工程队每天修公路多少米？

    （2）分别求甲、乙工程队修公路的长度y（米）与施工时间x（天）之间的函数关系式．

    （3）若该项工程由甲、乙两工程队一直合作施工，需几天完成？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：三角形中，、分别是和的平分线，、相交于点（知识链接：三角形三个内角的和是180°。如图是三角形的一个内角）

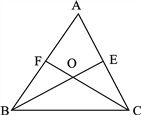
    （1）如果°求的度数。

    （2）如果°直接写出的度数

    （3）探求和的关系（用等式表示），并简要说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为发展校园足球运动，某县城区四校决定联合购买一批足球运动装备，市场调查发现：甲、乙两商场以同样的价格出售同种品牌的足球队服和足球，已知每套队服比每个足球多50元，两套队服与三个足球的费用相等，经洽谈，甲商场优惠方案是：每购买十套队服，送一个足球；乙商场优惠方案是：若购买队服超过80套，则购买足球打八折．

    （1）求每套队服和每个足球的价格是多少？

    （2）若城区四校联合购买100套队服和a个足球，请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用；

    （3）假如你是本次购买任务的负责人，你认为到哪家商场购买比较合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

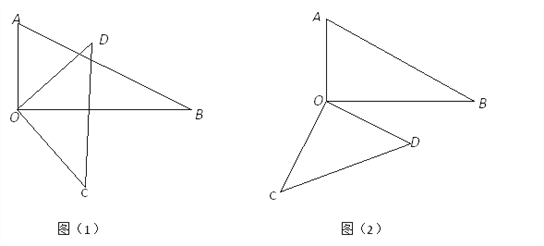
    【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起．

    （1）如图（1）若∠BOD=35°，求∠AOC的度数，若∠AOC=135°，求∠BOD的度数。

    （2）如图（2）若∠AOC=150°，求∠BOD的度数

    （3）猜想∠AOC与∠BOD的数量关系，并结合图（1）说明理由．

    （4）三角尺AOB不动，将三角尺COD的OD边与OA边重合，然后绕点O按顺时针或逆时针方向任意转动一个角度，当∠AOD（0°＜∠AOD＜90°）等于多少度时，这两块三角尺各有一条边互相垂直，直接写出∠AOD角度所有可能的值，不用说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=8，BC=6，点E在边AB上，点F在边CD上，点G、H在对角线AC上，若四边形EGFH是菱形，则AE的长是（ ）
    A.6
    B.6.25
    C.6.5
    D.7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2016年9月28日-12月31日，山东临沂灯展中千万盏彩灯点亮300亩天然花海．某日，从晚上17时开始每小时进入灯展的人数约为900人（之前该灯展有游客400人），同时每小时走出灯展的人数约为600人，已知该灯展的饱和人数约为1600人，则该灯展人数饱和时的时间约为（　　）

    A. 21时 B. 22时 C. 23时 D. 24时

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，抛物线y=ax2+2xa+c经过A（﹣4，0），B（0，4）两点，与x轴交于另一点C，直线y=x+5与x轴交于点D，与y轴交于点E．

    （1）求抛物线的解析式；
    （2）点P是第二象限抛物线上的一个动点，连接EP，过点E作EP的垂线l，在l上截取线段EF，使EF=EP，且点F在第一象限，过点F作FM⊥x轴于点M，设点P的横坐标为t，线段FM的长度为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；
    （3）在（2）的条件下，过点E作EH⊥ED交MF的延长线于点H，连接DH，点G为DH的中点，当直线PG经过AC的中点Q时，求点F的坐标．

    查看答案和解析>>

    同步练习册答案