
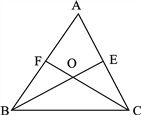
【题目】如图:三角形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的平分线,
的平分线,![]() 、
、![]() 相交于点
相交于点![]() (知识链接:三角形三个内角的和是180°。如图
(知识链接:三角形三个内角的和是180°。如图![]() 是三角形
是三角形![]() 的一个内角)
的一个内角)
(1)如果![]() °求
°求![]() 的度数。
的度数。
(2)如果![]() °直接写出
°直接写出![]() 的度数
的度数
(3)探求![]() 和
和![]() 的关系(用等式表示),并简要说明理由。
的关系(用等式表示),并简要说明理由。
【答案】(1)![]() 的度数为110°;
的度数为110°;
(2)![]() 的度数为115°;
的度数为115°;
(3)∠BOC=90°+![]() ∠A,理由见解析.
∠A,理由见解析.
【解析】
(1)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再根据角平分线的性质可求出∠EBC+∠FCB的度数,再由三角形的内角和为180°即可解答;
(2)同(1),根据三角形的内角和定理及角平分线的性质解答即可;
(3)根据(1)的叙述写出结论即可.
解:(1)∵∠A+∠ABC+∠ACB=180°,∠A=40°,
∴∠ABC+∠ACB=180°-∠A=140°,
∵∠EBC=![]() ∠ABC∠FCB=
∠ABC∠FCB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠FCB=![]() (∠ABC+∠ACB)=70°,
(∠ABC+∠ACB)=70°,
∴∠BOC=180°-70°=110°;
(2)同(1)∠BOC=180°-![]() =180°-
=180°-![]() =115°;
=115°;
(3)由(1)可知:∠BOC=90°+![]() ∠A,
∠A,
理由同(1),∵∠A+∠ABC+∠ACB=180°,BE、CF分别是∠ABC、∠ACB的平分线,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∴∠OBC+∠OCB=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A,
∠A,
∵∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-90°+![]() ∠A=90°+
∠A=90°+![]() ∠A.
∠A.
“点睛”本题考查的是三角形内角和定理及角平分线的性质,比较简单.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】![]() 为直线
为直线![]() 上一点,以
上一点,以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 平分
平分![]() .
.
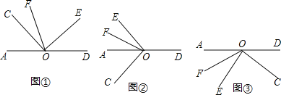
![]() 如图①,
如图①,![]() 与
与![]() 的数量关系为________,
的数量关系为________,![]() 和
和![]() 的数量关系为_________;
的数量关系为_________;
![]() 若将
若将![]() 绕点
绕点![]() 旋转至图②的位置,
旋转至图②的位置,![]() 依然平分
依然平分![]() ,请写出
,请写出![]() 和
和![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
![]() 若将
若将![]() 绕点
绕点![]() 旋转至图③的位置,射线
旋转至图③的位置,射线![]() 依然平分
依然平分![]() ,请直接写出
,请直接写出![]() 和
和![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣x+a(a>0),当自变量x取p时的函数值小于0,那么当自变量x取p﹣1时的函数值( )
A.小于0
B.大于0
C.等于0
D.与0的大小关系不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段MN=3cm,在线段MN上取一点P,使PM=PN;延长线段MN到点A,使AN=![]() MN;延长线段NM到点B,使BN=3BM.
MN;延长线段NM到点B,使BN=3BM.
(1)根据题意,画出图形;
(2)求线段AB的长;
(3)试说明点P是哪些线段的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com