
【题目】解下列方程:
(1)x2﹣2x=0
(2)4x2﹣8x﹣1=0(用配方法)
(3)3x2﹣1=4x(用公式法)
【答案】
(1)
解:)x(x﹣2)=0,
∴x=0或x﹣2=0,
解得:x=0或x=2;
(2)
解:4x2﹣8x=1,
x2﹣2x+1= ![]() +1,即(x﹣1)2=
+1,即(x﹣1)2= ![]() ,
,
∴x﹣1=± ![]() ,
,
则x= ![]() ;
;
(3)
解:3x2﹣4x﹣1=0,
∵a=3,b=﹣4,c=﹣1,
∴△=16+4×3×1=28>0,
则x= ![]() =
= ![]() .
.
【解析】(1)因式分解法求解可得;(2)配方法求解可得;(3)公式法求解可得.
【考点精析】解答此题的关键在于理解配方法的相关知识,掌握左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题,以及对公式法的理解,了解要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】计算(直接写出结果):
(1)﹣2+5
(2)﹣17+(﹣3)
(3)(﹣10)﹣(-6)
(4)(﹣1![]() )×(﹣12)
)×(﹣12)
(5)﹣2×(﹣3)2
(6)﹣1![]() ÷(﹣5)
÷(﹣5)
(7)﹣1200+(﹣1)200
(8)﹣0.125×(﹣2)3
(9)|﹣![]() |
|
(10)(-![]() )3
)3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:三角形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的平分线,
的平分线,![]() 、
、![]() 相交于点
相交于点![]() (知识链接:三角形三个内角的和是180°。如图
(知识链接:三角形三个内角的和是180°。如图![]() 是三角形
是三角形![]() 的一个内角)
的一个内角)
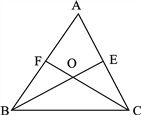
(1)如果![]() °求
°求![]() 的度数。
的度数。
(2)如果![]() °直接写出
°直接写出![]() 的度数
的度数
(3)探求![]() 和
和![]() 的关系(用等式表示),并简要说明理由。
的关系(用等式表示),并简要说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
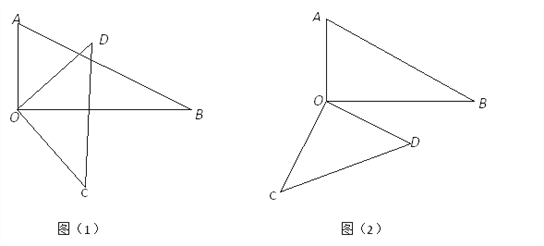
【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数。
(2)如图(2)若∠AOC=150°,求∠BOD的度数
(3)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是( ) 
A.6
B.6.25
C.6.5
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学文化课题活动中,把一副数学文化创意扑克牌中的4张扑克牌(如图所示)洗匀后正面向下放在桌面上,从中随机抽取2张牌,请你用列表或画树状图的方法,求抽取的2张牌的数字之和为偶数的概率. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月28日-12月31日,山东临沂灯展中千万盏彩灯点亮300亩天然花海.某日,从晚上17时开始每小时进入灯展的人数约为900人(之前该灯展有游客400人),同时每小时走出灯展的人数约为600人,已知该灯展的饱和人数约为1600人,则该灯展人数饱和时的时间约为( )
A. 21时 B. 22时 C. 23时 D. 24时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像经过点
的图像经过点![]() .
.
(1)求k的值,并判断点![]() 是否在该反比例函数的图像上;
是否在该反比例函数的图像上;
(2)该反比例函数图像在第______象限,在每个象限内,y随x的增大而_______.
(3)当![]() 时,求y的取值范围.
时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com