
����Ŀ����һ�����ǰ��е�����ֱ�����dzߵ�ֱ�Ƕ���O����ͼ��ʽ������һ��
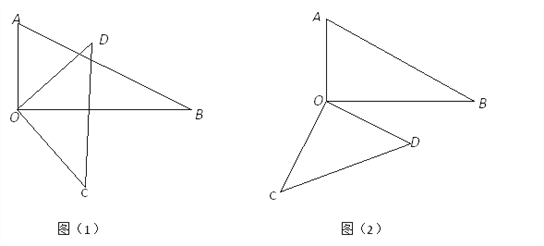
��1����ͼ��1������BOD=35�������AOC�Ķ���������AOC=135�������BOD�Ķ�����
��2����ͼ��2������AOC=150�������BOD�Ķ���
��3�������AOC���BOD��������ϵ�������ͼ��1��˵�����ɣ�
��4�����dz�AOB�����������dz�COD��OD����OA���غϣ�Ȼ���Ƶ�O��˳ʱ�����ʱ�뷽������ת��һ���Ƕȣ�����AOD��0�㣼��AOD��90�������ڶ��ٶ�ʱ�����������dz߸���һ�����ഹֱ��ֱ��д����AOD�Ƕ����п��ܵ�ֵ������˵�����ɣ�
���𰸡���1��45�㣻��2��30�㣻��2����ACB���DCE��������4��30��.45��.60��.75��
��������
����
(1)���ݡ�AOC����AOB����COD����BOD�ĺͲ��ϵ��⣻(2)���ܽǼ�ȥ��֪�ǵĶ�����(3)����(1)��(2)�еĽ�����룻(4)�������dz߸���һ�����ഹֱ��������ʽ����Ҫ��������.
�⣺(1)����BOD=35�㣬�ߡ�AOB=��COD=90�㣬
���AOC=��AOB+��COD����BOD=90��+90�㩁35��=145�㣬
����AOC=135�㣬
���BOD=��AOB+��COD����AOC=90��+90�㩁135��=45�㣻
(2)��ͼ2������AOC=150�㣬
���BOD=360�㩁��AOC����AOB����COD=30�㣻
(3)��AOC���BOD������
�ߡ�AOD+��BOD+��BOD+��BOC=180�㣮
�ߡ�AOD+��BOD+��BOC=��AOC��
���AOC+��BOD=180��������ACB���DCE������
(4)OD��ABʱ����AOD=30�㣬
CD��OBʱ����AOD=45�㣬
CD��ABʱ����AOD=75�㣬
OC��ABʱ����AOD=60�㣬
����AOD�Ƕ����п��ܵ�ֵΪ��30�㣻45�㣻60�㣻75��.


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪԭ�㣬��A��4��0������B��0��3�����ѡ�ABO�Ƶ�B��ʱ����ת���á�A��BO�䣬��A��O��ת��Ķ�Ӧ��ΪA�䡢O�䣬����ת��Ϊ����
��1����ͼ1������=90�㣬��AA��ij���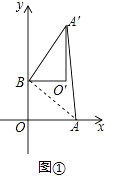
��2����ͼ2������=120�㣬���O������꣮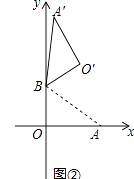
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2��x+a��a��0�������Ա���xȡpʱ�ĺ���ֵС��0����ô���Ա���xȡp��1ʱ�ĺ���ֵ�� ��
A.��0
B.����0
C.����0
D.��0�Ĵ�С��ϵ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB��AC����D�ڵױ�BC�ϣ��������������������ж���ABD�ա�ACD����(����)

A. BD��CD B. ��BAD����CAD C. ��B����C D. ��ADB����ADC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�MN��3cm�����߶�MN��ȡһ��P��ʹPM��PN���ӳ��߶�MN����A��ʹAN��![]() MN���ӳ��߶�NM����B��ʹBN��3BM.
MN���ӳ��߶�NM����B��ʹBN��3BM.
(1)�������⣬����ͼ�Σ�
(2)���߶�AB�ij���
(3)��˵����P����Щ�߶ε��е�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ABC��,AB=AC,��A=36��,DE��ֱƽ��AB��AC��D,��AB��E,��������������ǣ� ��

A. BDƽ����ABC B. D��AC���е�
C. AD=BD=BC D. ��BDC���ܳ�����AB+BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������з��̣�
��1��x2��2x=0
��2��4x2��8x��1=0�����䷽����
��3��3x2��1=4x���ù�ʽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һЩ��ͬ�ķ�����Ҫ��ˢǽ�棬һ��3��ʦ��ȥ��ˢ8�����䣬���������40�Oǽ��δ���ü�ˢ��ͬ��ʱ����5��ͽ�ܷ�ˢ��9�������ǽ�棬ÿ��ʦ����ͽ��һ���ˢ30�Oǽ�森
��1����ÿ��������Ҫ��ˢ��ǽ�������
��2�����ϰ�����36�������ķ�����Ҫ��ˢ,����1��ʦ����2��ͽ��ȥ,�輸�����?
��3����֪ÿ��ʦ����ͽ��ÿ��Ĺ��ʷֱ���85Ԫ��65Ԫ�����ϰ�Ҫ����3���ڣ�����3�죩���36������ķ�ˢ�����������8���й�����Ա����һ��8��ȫ�����ã����ź����أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ֽ���ʽ��![]() ��2���ֽ���ʽ�� 9a2��x��y��+4b2��y��x��
��2���ֽ���ʽ�� 9a2��x��y��+4b2��y��x��
��3���ֽ���ʽ��(x2��y2)2��4x2y2 ��4�����÷ֽ���ʽ������ֵ��2662-2342
��5�����÷ֽ���ʽ������ֵ����֪x-3y=-1��xy=2����x3y-6x2y2+9xy3��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com