
【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5 ![]() cm,且tan∠EFC=
cm,且tan∠EFC= ![]() ,则矩形ABCD的周长是 .
,则矩形ABCD的周长是 . 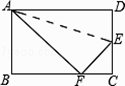
【答案】36cm
【解析】解:设CE=3k,则CF=4k,由勾股定理得EF=DE=5k, ∴DC=AB=8k,
∵∠AFB+∠BAF=90°,∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
∴tan∠BAF=tan∠EFC= ![]() ,
,
∴BF=6k,AF=BC=AD=10k,
在Rt△AFE中由勾股定理得AE= ![]() =
= ![]() =5
=5 ![]() ,
,
解得:k=1,
故矩形ABCD的周长=2(AB+BC)=2(8k+10k)=36cm.
根据tan∠EFC= ![]() 设CE=3k,在RT△EFC中可得CF=4k,EF=DE=5k,根据∠BAF=∠EFC,利用三角函数的知识求出AF,然后在RT△AEF中利用勾股定理求出k,继而代入可得出答案.
设CE=3k,在RT△EFC中可得CF=4k,EF=DE=5k,根据∠BAF=∠EFC,利用三角函数的知识求出AF,然后在RT△AEF中利用勾股定理求出k,继而代入可得出答案.


科目:初中数学 来源: 题型:
【题目】如图:三角形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的平分线,
的平分线,![]() 、
、![]() 相交于点
相交于点![]() (知识链接:三角形三个内角的和是180°。如图
(知识链接:三角形三个内角的和是180°。如图![]() 是三角形
是三角形![]() 的一个内角)
的一个内角)
(1)如果![]() °求
°求![]() 的度数。
的度数。
(2)如果![]() °直接写出
°直接写出![]() 的度数
的度数
(3)探求![]() 和
和![]() 的关系(用等式表示),并简要说明理由。
的关系(用等式表示),并简要说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月28日-12月31日,山东临沂灯展中千万盏彩灯点亮300亩天然花海.某日,从晚上17时开始每小时进入灯展的人数约为900人(之前该灯展有游客400人),同时每小时走出灯展的人数约为600人,已知该灯展的饱和人数约为1600人,则该灯展人数饱和时的时间约为( )
A. 21时 B. 22时 C. 23时 D. 24时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像经过点
的图像经过点![]() .
.
(1)求k的值,并判断点![]() 是否在该反比例函数的图像上;
是否在该反比例函数的图像上;
(2)该反比例函数图像在第______象限,在每个象限内,y随x的增大而_______.
(3)当![]() 时,求y的取值范围.
时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
(1)求AG的长;
(2)在坐标平面内存在点M(m,﹣1)使AM+CM最小,求出这个最小值;
(3)求线段GH所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)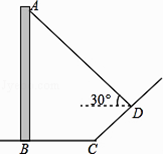
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+2xa+c经过A(﹣4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,连接EP,过点E作EP的垂线l,在l上截取线段EF,使EF=EP,且点F在第一象限,过点F作FM⊥x轴于点M,设点P的横坐标为t,线段FM的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点E作EH⊥ED交MF的延长线于点H,连接DH,点G为DH的中点,当直线PG经过AC的中点Q时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.

(1)求点B的坐标;
(2)在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级A班有50人,某次活动中分为四组,第一组有![]() 人,第二组是第一组的2倍多6人,第三组的人数等于第一组与第二组人数的和.
人,第二组是第一组的2倍多6人,第三组的人数等于第一组与第二组人数的和.
(1)第二组的人数 ,第三组的人数 ;(用含![]() 的式子表示)
的式子表示)
(2)求第四组的人数.(用含![]() 的式子表示)
的式子表示)
(3)试判断当a=7时,是否满足题意.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com