【题目】如图，折叠长方形的一边AD，使点D落在BC边上的点F处，BC=15，AB=9.
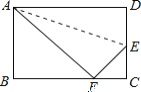
求：（1）FC的长；（2）EF的长．
【答案】（1）FC=3；（2）EF的长为5.
【解析】
（1）由折叠性质可得AF=AD，由勾股定理可求出BF的值，再由FC=BC-BF求解即可；
（2）由题意得EF=DE，设DE的长为x，则EC的长为（9-x）cm，在Rt△EFC中，由勾股定理即可求得EF的值.
解：(1)∵矩形对边相等，
∴AD=BC=15
∵折叠长方形的一边AD，点D落在BC边上的点F处
∴AF=AD=15，
在Rt△ABF中，由勾股定理得，
∴FC=BC·BF=15-12=3
(2)折叠长方形的一边AD，点D落在BC边上的点F处
∴EF=DE
设DE=x，则EC=9·x，
在Rt△EFC中，由勾股定理得，
即
解得x=5
即EF的长为5。
捷径训练检测卷系列答案
小夫子全能检测系列答案科目：初中数学 来源： 题型：
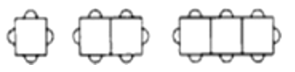
【题目】按下图方式摆放餐桌和椅子，
…
（1）1张长方形餐桌可坐4人，2张长方形餐桌拼在一起可坐______人．
（2）按照上图的方式继续排列餐桌，完成下表．
桌子张数 | 3 | 4 | 5 | n |
可坐人数 | ______ | ______ | ______ | ______ |
（3）一家餐厅有40张这样的长方形餐桌，某用餐单位要求餐厅按照上图方式，每8张长方形餐桌拼成1张大桌子，则该餐厅此时能容纳多少人用餐？
查看答案和解析>>
科目：初中数学 来源： 题型：
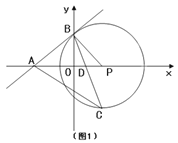
【题目】如图1，点A、B、P分别在两坐标轴上，∠APB=60°，PB=m，PA=2m，以点P为圆心、PB为半径作⊙P，作∠OBP的平分线分别交⊙P、OP于C、D，连接AC．
（1）求证：直线AB是⊙P的切线．
（2）设△ACD的面积为S，求S关于m的函数关系式．
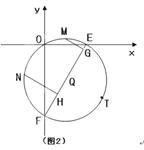
（3）如图2，当m=2时，把点C向右平移一个单位得到点T，过O、T两点作⊙Q交x轴、y轴于E、F两点，若M、N分别为两弧
的中点，作MG⊥EF，NH⊥EF，垂足为G、H，试求MG+NH的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知二次函数
的图象顶点在
轴上，且
，与一次函数
的图象交于
轴上一点
和另一交点
.
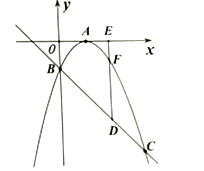
求抛物线的解析式；
点
为线段
上一点，过点作
轴，垂足为
，交抛物线于点
，请求出线段
的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，圆内接四边形ABCD两组对边的延长线分别相交于点E，F，且∠A=55°，∠E=30°，则∠F=_____．
【答案】40°
【解析】试题分析：先根据三角形外角性质计算出∠EBF=∠A+∠E=85°，再根据圆内接四边形的性质计算出∠BCD=180°﹣∠A=125°，然后再根据三角形外角性质求∠F．
解：∵∠A=55°，∠E=30°，
∴∠EBF=∠A+∠E=85°，
∵∠A+∠BCD=180°，
∴∠BCD=180°﹣55°=125°，
∵∠BCD=∠F+∠CBF，
∴∠F=125°﹣85°=40°．
故答案为40°．
考点：圆内接四边形的性质；三角形内角和定理．
【题型】填空题
【结束】
17
【题目】某果园有100棵橘子树，平均每一棵树结600个橘子．根据经验估计，每多种一棵树，平均每棵树就会少结5个橘子．设果园增种x棵橘子树，果园橘子总个数为y个，则果园里增种 棵橘子树，橘子总个数最多．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AD//BC，∠A=∠C，CD=2AD，BE⊥AD于点E，F为CD的中点，连接EF、BF．
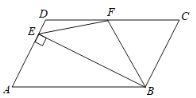
（1）求证：四边形ABCD是平行四边形；
（2）求证：BF平分∠ABC；
（3）请判断△BEF的形状，并证明你的结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在正方形ABCD内作∠EAF=45°，AE交BC于点E，AF交CD于点F，连接EF，过点A作AH⊥EF，垂足为H．
（1）如图2，将△ADF绕点A顺时针旋转90°得到△ABG．
①求证：△AGE≌△AFE；
②若BE=2，DF=3，求AH的长．
（2）如图3，连接BD交AE于点M，交AF于点N．请探究并猜想：线段BM，MN，ND之间有什么数量关系？并说明理由．
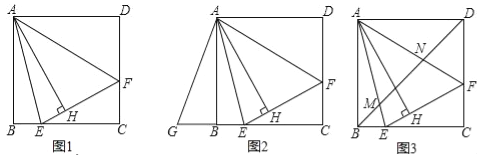
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知正方形ABCD，点P是对角线AC所在直线上的动点，点E在DC边所在直线上，且随着点P的运动而运动，PE=PD总成立。
(1)如图(1),当点P在对角线AC上时,请你通过测量、观察,猜想PE与PB有怎样的关系?(直接写出结论不必证明)；
(2)如图(2),当点P运动到CA的延长线上时,(1)中猜想的结论是否成立?如果成立，请给出证明；如果不成立，请说明理由；
(3)如图(3),当点P运动到CA的反向延长线上时,请你利用图(3)画出满足条件的图形,并判断此时PE与PB有怎样的关系?(直接写出结论不必证明)
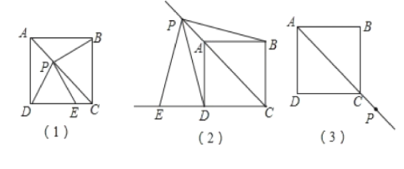
查看答案和解析>>
科目：初中数学 来源： 题型：
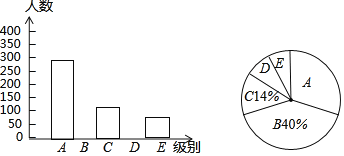
【题目】某报社为了了解市民“获取新闻的最主要途径”，开展了一次抽样调查，根据调查结果绘制了如图三种不完整的统计图表．
组别 | 获取新闻的最主要途径 | 人数 |
A | 电脑上网 | 280 |
B | 手机上网 | m |
C | 电视 | 140 |
D | 报纸 | n |
E | 其它 | 80 |
请根据图表信息解答下列问题：
（1）统计表中的m＝ ，n＝ ，并请补全条形统计图；
（2）扇形统计图中“D”所对应的圆心角的度数是 ；
（3）若该市约有120万人，请你估计其中将“电脑上网”和“手机上网”作为“获取新闻的最主要途径”的总人数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com