练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知二次函数的图象顶点在轴上，且，与一次函数的图象交于轴上一点和另一交点.

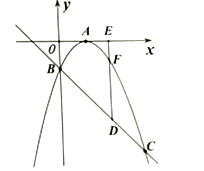
    求抛物线的解析式；

    点为线段上一点，过点作轴，垂足为，交抛物线于点，请求出线段的最大值.

    【答案】(1) ；（2）线段的最大值为.

    【解析】

    （1）根据题意首先计算A、B点的坐标，设出二次函数的解析式，代入求出参数即可.

    （2）根据题意设F点的横坐标为m,再结合抛物线和一次函数的解析式即可表示F、D的纵坐标，所以可得DF的长度，使用配方法求解出最大值即可.

    解：，二次函数与一次函数的图象交于轴上一点，

    点为，点为.

    二次函数的图象顶点在轴上.

    设二次函数解析式为.

    把点代入得，

    .

    抛物线的解析式为，即.

    设点坐标为，点坐标为.

    .

    当时，即，解得.

    点为线段上一点,

    .

    当时，线段的最大值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】定义：若线段上的一个点把这条线段分成1：2的两条线段，则称这个点是这条线段的三等分点．如图1，点C在线段AB上，且AC：CB＝1：2，则点C是线段AB的一个三等分点，显然，一条线段的三等分点有两个．

    （1）已知：如图2，DE＝15cm，点P是DE的三等分点，求DP的长．

    （2）已知，线段AB＝15cm，如图3，点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动；点Q从点B出发，先向点A方向运动，当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm，设运动时间为t秒．

    ①若点P点Q同时出发，且当点P与点Q重合时，求t的值．

    ②若点P点Q同时出发，且当点P是线段AQ的三等分点时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中,规定：抛物线y=a(xh) +k的关联直线为y=a(xh)+k.

    例如：抛物线y=2(x+1) 3的关联直线为y=2(x+1)3，即y=2x1.

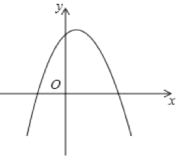
    (1)如图,对于抛物线y=(x1) +3.

    ①该抛物线的顶点坐标为___，关联直线为___，该抛物线与其关联直线的交点坐标为___和___；

    ②点P是抛物线y=(x1) +3上一点,过点P的直线PQ垂直于x轴,交抛物线y=(x1) +3的关联直线于点Q.设点P的横坐标为m,线段PQ的长度为d(d>0)，求当d随m的增大而减小时，d与m之间的函数关系式，并写出自变量m的取值范围。

    (2)顶点在第一象限的抛物线y=a(x1) +4a与其关联直线交于点A,B(点A在点B的左侧)，与x轴负半轴交于点C，直线AB与x轴交于点D，连结AC、BC.

    ①求△BCD的面积(用含a的代数式表示).

    ②当△ABC为钝角三角形时，直接写出a的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（2017浙江省湖州市，第23题，10分）湖州素有鱼米之乡之称，某水产养殖大户为了更好地发挥技术优势，一次性收购了20000kg淡水鱼，计划养殖一段时间后再出售．已知每天放养的费用相同，放养10天的总成本为30.4万元；放养20天的总成本为30.8万元（总成本=放养总费用+收购成本）．

    （1）设每天的放养费用是a万元，收购成本为b万元，求a和b的值；

    （2）设这批淡水鱼放养t天后的质量为m（kg），销售单价为y元/kg．根据以往经验可知：m与t的函数关系为；y与t的函数关系如图所示．

    ①分别求出当0≤t≤50和50＜t≤100时，y与t的函数关系式；

    ②设将这批淡水鱼放养t天后一次性出售所得利润为W元，求当t为何值时，W最大？并求出最大值．（利润=销售总额﹣总成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数的图象如图，则下列结论中正确的有（　　）

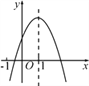
    ①a＋b＋c＞0；②a－b＋c＜0；③b＞0；④b＝2a；⑤abc＜0.

    A. 5个 B. 4个 C. 3个 D. 2个

    【答案】B

    【解析】试题解析：当x=1时，y=a+b+c，顶点坐标（1，a+b+c），

    由图象可知，顶点坐标在第一象限，

    ∴a+b+c＞0，故①正确；

    当x=-1时，y=a-b+c，

    由图象可知，当x=-1时，所对应的点在第四象限，

    ∴y=a-b+c＜0，故②正确；

    ∵图象开口向下，

    ∴a＜0，

    ∵x=- =1，

    ∴b=-2a，故④错误；

    ∴b＞0，故③正确；

    ∵图象与y轴的交点在y轴的上半轴，

    ∴c＞0，

    ∴abc＜0，故⑤正确；

    ∴正确的有4个．

    故选B．

    【题型】单选题
    【结束】
    10

    【题目】如图，在△ABC中，∠B＝∠C＝36°，AB的垂直平分线交BC于点D，交AB于点H，AC的垂直平分线交BC于点E，交AC于点G，连接AD，AE，则下列结论错误的是( )

    A. B. AD，AE将∠BAC三等分

    C. △ABE≌△ACD D. S△ADH＝S△CEG

    查看答案和解析>>

    科目：初中数学 来源： 题型：

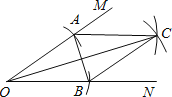
    【题目】如图，在∠MON的两边上分别截取OA、OB，使OA=OB；分别以点A、B为圆心，OA长为半径作弧，两弧交于点C，连接AC、BC、AB、OC．若AB=2cm，四边形OACB的周长为8cm．则OC的长为______cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，折叠长方形的一边AD，使点D落在BC边上的点F处，BC=15，AB=9.

    求：（1）FC的长；（2）EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

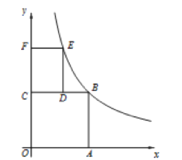
    【题目】如图，正方形OABC的边OA，OC在坐标轴上，矩形CDEF的边CD在CB上，且5CD=3CB，边CF在轴上，且CF=2OC-3，反比例函数y= (k>0)的图象经过点B,E，则点E的坐标是____

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，函数的图象与函数的图象交于点，.

    (1)求函数的表达式；

    (2)观察图象，直接写出不等式的解集；

    (3)若点是轴上的动点，当周长最小时，求点的坐标.

    查看答案和解析>>

    同步练习册答案