
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§ЕФЭМЯѓШчЭМЃЌдђЯТСаНсТлжае§ШЗЕФгаЃЈЁЁЁЁЃЉ
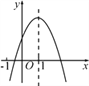
ЂйaЃЋbЃЋcЃО0ЃЛЂкaЃbЃЋcЃМ0ЃЛЂлbЃО0ЃЛЂмbЃН2aЃЛЂнabcЃМ0.
A. 5Иі B. 4Иі C. 3Иі D. 2Иі
ЁОД№АИЁПB
ЁОНтЮіЁПЪдЬтНтЮіЃКЕБx=1ЪБЃЌy=a+b+cЃЌЖЅЕузјБъЃЈ1ЃЌa+b+cЃЉЃЌ
гЩЭМЯѓПЩжЊЃЌЖЅЕузјБъдкЕквЛЯѓЯоЃЌ
Ёрa+b+cЃО0ЃЌЙЪЂйе§ШЗЃЛ
ЕБx=-1ЪБЃЌy=a-b+cЃЌ
гЩЭМЯѓПЩжЊЃЌЕБx=-1ЪБЃЌЫљЖдгІЕФЕудкЕкЫФЯѓЯоЃЌ
Ёрy=a-b+cЃМ0ЃЌЙЪЂке§ШЗЃЛ
ЁпЭМЯѓПЊПкЯђЯТЃЌ
ЁрaЃМ0ЃЌ
Ёпx=-![]() =1ЃЌ
=1ЃЌ
Ёрb=-2aЃЌЙЪЂмДэЮѓЃЛ
ЁрbЃО0ЃЌЙЪЂле§ШЗЃЛ
ЁпЭМЯѓгыyжсЕФНЛЕудкyжсЕФЩЯАыжсЃЌ
ЁрcЃО0ЃЌ
ЁрabcЃМ0ЃЌЙЪЂне§ШЗЃЛ
Ёре§ШЗЕФга4ИіЃЎ
ЙЪбЁBЃЎ
ЁОЬтаЭЁПЕЅбЁЬт
ЁОНсЪјЁП
10
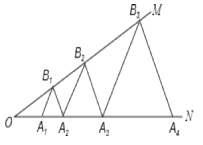
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBЃНЁЯCЃН36ЁуЃЌABЕФДЙжБЦНЗжЯпНЛBCгкЕуDЃЌНЛABгкЕуHЃЌACЕФДЙжБЦНЗжЯпНЛBCгкЕуEЃЌНЛACгкЕуGЃЌСЌНгADЃЌAEЃЌдђЯТСаНсТлДэЮѓЕФЪЧ( )

A. ![]() B. ADЃЌAEНЋЁЯBACШ§ЕШЗж
B. ADЃЌAEНЋЁЯBACШ§ЕШЗж
C. ЁїABEЁеЁїACD D. SЁїADHЃНSЁїCEG
ЁОД№АИЁПA
ЁОНтЮіЁПЪдЬтНтЮіЃКЁпЁЯB=ЁЯC=36ЁуЃЌЁрAB=ACЃЌЁЯBAC=108ЁуЃЌЁпDHДЙжБЦНЗжABЃЌEGДЙжБЦНЗжACЃЌЁрDB=DAЃЌEA=ECЃЌЁрЁЯB=ЁЯDAB=ЁЯC=ЁЯCAE=36ЁуЃЌЁрЁїBDAЁзЁїBACЃЌЁр![]() ЃЌгжЁпЁЯADC=ЁЯB+ЁЯBAD=72ЁуЃЌЁЯDAC=ЁЯBACЉЁЯBAD=72ЁуЃЌЁрЁЯADC=ЁЯDACЃЌЁрCD=CA=BAЃЌЁрBD=BCЉCD=BCЉABЃЌдђ
ЃЌгжЁпЁЯADC=ЁЯB+ЁЯBAD=72ЁуЃЌЁЯDAC=ЁЯBACЉЁЯBAD=72ЁуЃЌЁрЁЯADC=ЁЯDACЃЌЁрCD=CA=BAЃЌЁрBD=BCЉCD=BCЉABЃЌдђ![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌЙЪAДэЮѓЃЛ
ЃЌЙЪAДэЮѓЃЛ
ЁпЁЯBAC=108ЁуЃЌЁЯB=ЁЯDAB=ЁЯC=ЁЯCAE=36ЁуЃЌЁрЁЯDAE=ЁЯBACЉЁЯDABЉЁЯCAE=36ЁуЃЌМДЁЯDAB=ЁЯDAE=ЁЯCAE=36ЁуЃЌЁрADЃЌAEНЋЁЯBACШ§ЕШЗжЃЌЙЪBе§ШЗЃЛ
ЁпЁЯBAE=ЁЯBAD+ЁЯDAE=72ЁуЃЌЁЯCAD=ЁЯCAE+ЁЯDAE=72ЁуЃЌЁрЁЯBAE=ЁЯCADЃЌдкЁїBAEКЭЁїCADжаЃЌЁпЁЯB=ЁЯCЃЌAB=ACЃЌЁЯBAE=ЁЯCADЃЌЁрЁїBAEЁеЁїCADЃЌЙЪCе§ШЗЃЛ
гЩЁїBAEЁеЁїCADПЩЕУSЁїBAE=SЁїCADЃЌМДSЁїBAD+SЁїADE=SЁїCAE+SЁїADEЃЌЁрSЁїBAD=SЁїCAEЃЌгжЁпDHДЙжБЦНЗжABЃЌEGДЙжБЦНЗжACЃЌЁрSЁїADH=![]() SЁїABDЃЌSЁїCEG=
SЁїABDЃЌSЁїCEG=![]() SЁїCAEЃЌЁрSЁїADH=SЁїCEGЃЌЙЪDе§ШЗЃЎ
SЁїCAEЃЌЁрSЁїADH=SЁїCEGЃЌЙЪDе§ШЗЃЎ
ЙЪбЁAЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,вбжЊЃКЁЯMON=30Ёу,ЕуA![]() ЁЂA
ЁЂA![]() ЁЂA
ЁЂA![]() ЁдкЩфЯпONЩЯ,ЕуB
ЁдкЩфЯпONЩЯ,ЕуB![]() ЁЂB
ЁЂB![]() ЁЂB
ЁЂB![]() ЁдкЩфЯпOMЩЯ,ЁїA
ЁдкЩфЯпOMЩЯ,ЁїA![]() B
B![]() A
A![]() ЁЂЁїA
ЁЂЁїA![]() B
B![]() A
A![]() ЁЂЁїA
ЁЂЁїA![]() B
B![]() A
A![]() ЁОљЮЊЕШБпШ§НЧаЮ,ШєOA
ЁОљЮЊЕШБпШ§НЧаЮ,ШєOA![]() =1,дђЁїA
=1,дђЁїA![]() B
B![]() A
A![]() ЕФБпГЄЮЊ____
ЕФБпГЄЮЊ____
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋвЛеХе§ЗНаЮжНЦЌМєГЩЫФеХДѓаЁвЛбљЕФаЁе§ЗНаЮжНЦЌЃЌШЛКѓНЋЦфжавЛеХе§ЗНаЮжНЦЌдйАДЭЌбљЗНЗЈМєГЩЫФеХаЁе§ЗНаЮжНЦЌЃЌдйНЋЦфжавЛеХМєГЩЫФеХаЁе§ЗНаЮжНЦЌЃЌШчДЫНјааЯТШЅ.
ЃЈ1ЃЉЬюБэЃК
МєЕФДЮЪ§ | 1 | 2 | 3 | 4 | 5 |
жНЦЌеХЪ§ | 4 | 7 |
ЃЈ2ЃЉШчЙћМєСЫ100ДЮЃЌЙВМєГіЖрЩйеХжНЦЌЃП
ЃЈ3ЃЉШчЙћМєСЫ![]() ДЮЃЌЙВМєГіЖрЩйеХжНЦЌЃП
ДЮЃЌЙВМєГіЖрЩйеХжНЦЌЃП
ЃЈ4ЃЉФмЗёМєШєИЩДЮКѓЙВЕУЕН2019еХжНЦЌЃПШєФмЃЌЧыжБНгаДГіЯргІМєЕФДЮЪ§ЃЛШєВЛФмЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
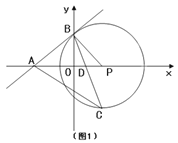
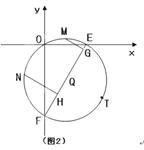
ЁОЬтФПЁПШчЭМ1ЃЌЕуAЁЂBЁЂPЗжБ№дкСНзјБъжсЩЯЃЌЁЯAPB=60ЁуЃЌPB=mЃЌPA=2mЃЌвдЕуPЮЊдВаФЁЂPBЮЊАыОЖзїЁбPЃЌзїЁЯOBPЕФЦНЗжЯпЗжБ№НЛЁбPЁЂOPгкCЁЂDЃЌСЌНгACЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпABЪЧЁбPЕФЧаЯпЃЎ
ЃЈ2ЃЉЩшЁїACDЕФУцЛ§ЮЊSЃЌЧѓSЙигкmЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌЕБm=2ЪБЃЌАбЕуCЯђгвЦНвЦвЛИіЕЅЮЛЕУЕНЕуTЃЌЙ§OЁЂTСНЕузїЁбQНЛxжсЁЂyжсгкEЁЂFСНЕуЃЌШєMЁЂNЗжБ№ЮЊСНЛЁ![]() ЕФжаЕуЃЌзїMGЁЭEFЃЌNHЁЭEFЃЌДЙзуЮЊGЁЂHЃЌЪдЧѓMG+NHЕФжЕЃЎ
ЕФжаЕуЃЌзїMGЁЭEFЃЌNHЁЭEFЃЌДЙзуЮЊGЁЂHЃЌЪдЧѓMG+NHЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌPЕуДгЕуAПЊЪМвд2РхУз/УыЕФЫйЖШбиAЁњBЁњCЕФЗНЯђвЦЖЏЃЌЕуQДгЕуCПЊЪМвд1РхУз/УыЕФЫйЖШбиCЁњAЁњBЕФЗНЯђвЦЖЏЃЌдкжБНЧШ§НЧаЮABCжаЃЌЁЯAЃН90ЁуЃЌШєABЃН16РхУзЃЌACЃН12РхУзЃЌBCЃН20РхУзЃЌШчЙћPЁЂQЭЌЪБГіЗЂЃЌгУtЃЈУыЃЉБэЪОвЦЖЏЪБМфЃЌФЧУДЃК
ЃЈ1ЃЉШчЭМ1ЃЌШєPдкЯпЖЮABЩЯдЫЖЏЃЌQдкЯпЖЮCAЩЯдЫЖЏЃЌЪдЧѓГіtЮЊКЮжЕЪБЃЌQAЃНAP
ЃЈ2ЃЉШчЭМ2ЃЌЕуQдкCAЩЯдЫЖЏЃЌЪдЧѓГіtЮЊКЮжЕЪБЃЌШ§НЧаЮQABЕФУцЛ§ЕШгкШ§НЧаЮABCУцЛ§ЕФ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБPЕуЕНДяCЕуЪБЃЌPЁЂQСНЕуЖМЭЃжЙдЫЖЏЃЌЪдЧѓЕБtЮЊКЮжЕЪБЃЌЯпЖЮAQЕФГЄЖШЕШгкЯпЖЮBPЕФГЄЕФ![]()

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓЖЅЕудк
ЕФЭМЯѓЖЅЕудк![]() жсЩЯЃЌЧв
жсЩЯЃЌЧв![]() ЃЌгывЛДЮКЏЪ§
ЃЌгывЛДЮКЏЪ§![]() ЕФЭМЯѓНЛгк
ЕФЭМЯѓНЛгк![]() жсЩЯвЛЕу
жсЩЯвЛЕу![]() КЭСэвЛНЛЕу
КЭСэвЛНЛЕу![]() .
.
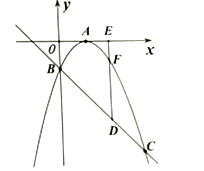
![]() ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
![]() Еу
Еу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЕуЃЌЙ§Еу
ЩЯвЛЕуЃЌЙ§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЌНЛХзЮяЯпгкЕу
ЃЌНЛХзЮяЯпгкЕу![]() ЃЌЧыЧѓГіЯпЖЮ
ЃЌЧыЧѓГіЯпЖЮ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдВФкНгЫФБпаЮABCDСНзщЖдБпЕФбгГЄЯпЗжБ№ЯрНЛгкЕуEЃЌFЃЌЧвЁЯA=55ЁуЃЌЁЯE=30ЁуЃЌдђЁЯF=_____ЃЎ

ЁОД№АИЁП40Ёу
ЁОНтЮіЁПЪдЬтЗжЮіЃКЯШИљОнШ§НЧаЮЭтНЧаджЪМЦЫуГіЁЯEBF=ЁЯA+ЁЯE=85ЁуЃЌдйИљОндВФкНгЫФБпаЮЕФаджЪМЦЫуГіЁЯBCD=180ЁуЉЁЯA=125ЁуЃЌШЛКѓдйИљОнШ§НЧаЮЭтНЧаджЪЧѓЁЯFЃЎ
НтЃКЁпЁЯA=55ЁуЃЌЁЯE=30ЁуЃЌ
ЁрЁЯEBF=ЁЯA+ЁЯE=85ЁуЃЌ
ЁпЁЯA+ЁЯBCD=180ЁуЃЌ
ЁрЁЯBCD=180ЁуЉ55Ёу=125ЁуЃЌ
ЁпЁЯBCD=ЁЯF+ЁЯCBFЃЌ
ЁрЁЯF=125ЁуЉ85Ёу=40ЁуЃЎ
ЙЪД№АИЮЊ40ЁуЃЎ
ПМЕуЃКдВФкНгЫФБпаЮЕФаджЪЃЛШ§НЧаЮФкНЧКЭЖЈРэЃЎ
ЁОЬтаЭЁПЬюПеЬт
ЁОНсЪјЁП
17
ЁОЬтФПЁПФГЙћдАга100ПУщйзгЪїЃЌЦНОљУПвЛПУЪїНс600ИіщйзгЃЎИљОнОбщЙРМЦЃЌУПЖржжвЛПУЪїЃЌЦНОљУППУЪїОЭЛсЩйНс5ИіщйзгЃЎЩшЙћдАдіжжxПУщйзгЪїЃЌЙћдАщйзгзмИіЪ§ЮЊyИіЃЌдђЙћдАРядіжж ПУщйзгЪїЃЌщйзгзмИіЪ§зюЖрЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
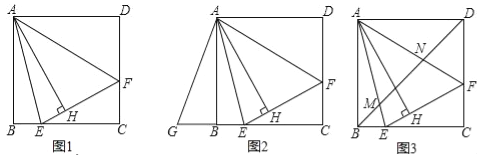
ЁОЬтФПЁПШчЭМ1ЃЌдке§ЗНаЮABCDФкзїЁЯEAF=45ЁуЃЌAEНЛBCгкЕуEЃЌAFНЛCDгкЕуFЃЌСЌНгEFЃЌЙ§ЕуAзїAHЁЭEFЃЌДЙзуЮЊHЃЎ
ЃЈ1ЃЉШчЭМ2ЃЌНЋЁїADFШЦЕуAЫГЪБеыа§зЊ90ЁуЕУЕНЁїABGЃЎ
ЂйЧѓжЄЃКЁїAGEЁеЁїAFEЃЛ
ЂкШєBE=2ЃЌDF=3ЃЌЧѓAHЕФГЄЃЎ
ЃЈ2ЃЉШчЭМ3ЃЌСЌНгBDНЛAEгкЕуMЃЌНЛAFгкЕуNЃЎЧыЬНОПВЂВТЯыЃКЯпЖЮBMЃЌMNЃЌNDжЎМфгаЪВУДЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСНИљФОЬѕЃЌвЛИљГЄ20cmЃЌСэвЛИљГЄ24cmЃЌНЋЫќУЧвЛЖЫжиКЯЧвЗХдкЭЌвЛЬѕжБЯпЩЯЃЌДЫЪБСНИљФОЬѕЕФжаЕужЎМфЕФОрРыЮЊ(ЁЁЁЁ)
A. 2cm B. 4cm C. 2cmЛђ22cm D. 4cmЛђ44cm
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com