
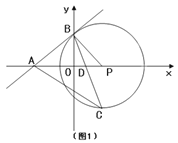
����Ŀ����ͼ1����A��B��P�ֱ������������ϣ���APB=60�㣬PB=m��PA=2m���Ե�PΪԲ�ġ�PBΪ�뾶����P������OBP��ƽ���߷ֱ���P��OP��C��D������AC��
��1����֤��ֱ��AB����P�����ߣ�
��2������ACD�����ΪS����S����m�ĺ�����ϵʽ��
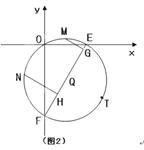
��3����ͼ2����m=2ʱ���ѵ�C����ƽ��һ����λ�õ���T����O��T��������Q��x�ᡢy����E��F���㣬��M��N�ֱ�Ϊ����![]() ���е㣬��MG��EF��NH��EF������ΪG��H������MG+NH��ֵ��
���е㣬��MG��EF��NH��EF������ΪG��H������MG+NH��ֵ��
���𰸡�������
������������: ��1���������ߵ��ж�����֤�á�ABP=90�����ж����ߣ�
��2������PC�����ݡ�APB=90��-��OBP=��OBA����OBC=��PBC���õ���ADB=��PBC+��PBC=��ABD���Ӷ��õ���CPA=��POB=90�������������ε������ʽ�õ�S=![]() m2��
m2��
��3����TJ��x�ᣬTK��y�ᣬ����ET��FT���õ���ETJ�ա�FTK���Ӷ��õ�NH=![]() NR=
NR=![]() OF��MG=
OF��MG=![]() OE��������MG+NH=
OE��������MG+NH=![]() ��OE+OF��=
��OE+OF��=![]() ��4=2.
��4=2.
���:
��1���ߡ�POB=90�㣬��APB=60�㣬
��PB=m��
��PO=![]() PB=
PB=![]() m��OB=
m��OB=![]() m��
m��
�֡�PA=2m��
��OA=![]() m��
m��
��RT��OAB��AB=![]() m
m
��PA2+AB2=PA2
���ABP=90�㣬
��PB�ǡ�P�İ뾶��
��ֱ��AB�ǡ�P�����ߣ�
��2������PC��
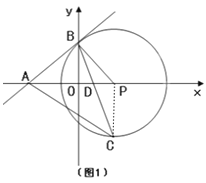
�ߡ�APB=90��-��OBP=��OBA����OBC=��PBC��
���ADB=��PBC+��PBC=��ABD
��AD=AB=![]() m��
m��
�֡�PB=PC=m��
��PC��OC
���CPA=��POB=90�㣬
��S��ACD=![]() AD��CP=
AD��CP=![]()
![]() m��m=
m��m=![]() m2��
m2��
��3����TG��x�ᣬTK��y�ᣬ����ET��FT��
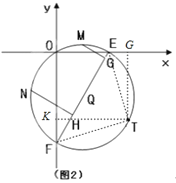
��m=2ʱ��PO=![]() m���ɣ�2��֪��CPA=90�㣬
m���ɣ�2��֪��CPA=90�㣬
��C��Ϊ ��1��-2����
��T��2��-2����TG=TK=2��
���T�ڡ�EOF��ƽ�����ϣ���![]()
��TE=TF��
���ETG�ա�FTK��
��EF=EG��
��OE+OF=OG-EG+OK+FK=OG+OK=4
�ӳ�NH����Q��R������QN��QR���ߡ�EOF=90�㣬
��EFΪ��Q��ֱ������![]()
![]()
![]()
��NR=OF
��NH=![]() NR=
NR=![]() OF
OF
ͬ��MG=![]() OE
OE
��MG+NH=![]() ��OE+OF��=
��OE+OF��=![]() ��4=2
��4=2
�㾦: ���⿼����Բ���ۺ�֪ʶ���ѶȽϴ�һ��Ϊ�п����ѹ����.


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
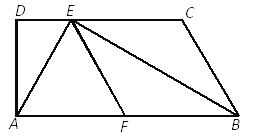
����Ŀ����ͼ����֪����ABCD�У�AB��CD����D=90�㣬BEƽ�֡�ABC����CD�ڵ�E��F��AB���е㣬����AE��EF����AE��BE��
��֤����1���ı���BCEF�����Σ�
��2��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ϴӼ����ܲ�ȥ�������������������һ��������ߵ��ľߵ�ȥ��ʣ�Ȼ���ؼң���ͼ��С����ҵľ���![]() ����λ��
����λ��![]() ����ʱ��
����ʱ��![]() ����λ��
����λ��![]() ����ͼ����ͼ��ش��������⣺
����ͼ����ͼ��ش��������⣺
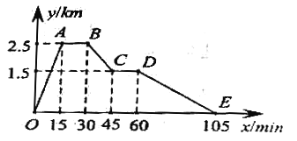
��1����������С�ϼ�______![]() ��
��
��2������������������______![]() ��
��
��3��С�ϴ��������ߵ��ľߵ��ƽ���ٶ���______![]() ��
��
��4��С���ڷ���ʱ����ʱ��ҵľ�����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ��,�涨��������y=a(xh) ![]() +k�Ĺ���ֱ��Ϊy=a(xh)+k.
+k�Ĺ���ֱ��Ϊy=a(xh)+k.
���磺������y=2(x+1) ![]() 3�Ĺ���ֱ��Ϊy=2(x+1)3����y=2x1.
3�Ĺ���ֱ��Ϊy=2(x+1)3����y=2x1.
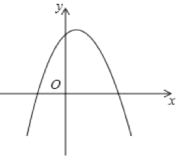
(1)��ͼ,����������y=(x1) ![]() +3.
+3.
�ٸ������ߵĶ�������Ϊ___������ֱ��Ϊ___�����������������ֱ�ߵĽ�������Ϊ___��___��
�ڵ�P��������y=(x1) ![]() +3��һ��,����P��ֱ��PQ��ֱ��x��,��������y=(x1)
+3��һ��,����P��ֱ��PQ��ֱ��x��,��������y=(x1)![]() +3�Ĺ���ֱ���ڵ�Q.���P�ĺ�����Ϊm,�߶�PQ�ij���Ϊd(d>0)����d��m���������Сʱ��d��m֮��ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
+3�Ĺ���ֱ���ڵ�Q.���P�ĺ�����Ϊm,�߶�PQ�ij���Ϊd(d>0)����d��m���������Сʱ��d��m֮��ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
(2)�����ڵ�һ����������y=a(x1) ![]() +4a�������ֱ�߽��ڵ�A,B(��A�ڵ�B�����)����x�Ḻ���ύ�ڵ�C��ֱ��AB��x�ύ�ڵ�D������AC��BC.
+4a�������ֱ�߽��ڵ�A,B(��A�ڵ�B�����)����x�Ḻ���ύ�ڵ�C��ֱ��AB��x�ύ�ڵ�D������AC��BC.
�����BCD�����(�ú�a�Ĵ���ʽ��ʾ).
�ڵ���ABCΪ�۽�������ʱ��ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��c=10����a��b����(a+26)2+|b+c|=0����ش����⣺
��1����ֱ��д��a��b��c��ֵ��a=�� ����b=�� ����
��2����������a��b��c����Ӧ�ĵ�ֱ�ΪA��B��C����A��B�����ľ���ΪAB����AB=�� ����AC=�� ����
��3���ڣ�1����2���������£�����M�ӵ�A��������ÿ��1����λ���ȵ��ٶ������˶�������M�����Cʱ����Mֹͣ������M�˶�����Bʱ����N�ӵ�A��������ÿ��3����λ���������˶�����N�����C����������ͬ�����ٶȷ��أ�����N�����Aʱ����Nֹͣ���ӵ�M��ʼ�˶�ʱ������M��N��ֹͣ�˶�Ϊֹ����ʱ��Ϊt�룬���ú�t�Ĵ���ʽ��ʾM��N�����ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017�㽭ʡ�����У���23�⣬10�֣�������������֮��֮�ƣ�ijˮ����ֳ��Ϊ�˸��õط��Ӽ������ƣ�һ�����չ���20000kg��ˮ�㣬�ƻ���ֳһ��ʱ����ٳ��ۣ���֪ÿ������ķ�����ͬ������10����ܳɱ�Ϊ30.4��Ԫ������20����ܳɱ�Ϊ30.8��Ԫ���ܳɱ�=�����ܷ���+�չ��ɱ�����
��1����ÿ��ķ���������a��Ԫ���չ��ɱ�Ϊb��Ԫ����a��b��ֵ��
��2����������ˮ�����t��������Ϊm��kg�������۵���ΪyԪ/kg���������������֪��m��t�ĺ�����ϵΪ![]() ��y��t�ĺ�����ϵ��ͼ��ʾ��
��y��t�ĺ�����ϵ��ͼ��ʾ��
�ٷֱ������0��t��50��50��t��100ʱ��y��t�ĺ�����ϵʽ��
���轫������ˮ�����t���һ���Գ�����������ΪWԪ����tΪ��ֵʱ��W���������ֵ��������=�����ܶ�ܳɱ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ�����ͼ����ͼ�������н�������ȷ���У�������
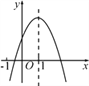
��a��b��c��0����a��b��c��0����b��0����b��2a����abc��0.
A. 5�� B. 4�� C. 3�� D. 2��
���𰸡�B
�������������������x=1ʱ��y=a+b+c���������꣨1��a+b+c����
��ͼ���֪�����������ڵ�һ���ޣ�
��a+b+c��0���ʢ���ȷ��
��x=-1ʱ��y=a-b+c��
��ͼ���֪����x=-1ʱ������Ӧ�ĵ��ڵ������ޣ�
��y=a-b+c��0���ʢ���ȷ��
��ͼ�����£�
��a��0��
��x=-![]() =1��
=1��
��b=-2a���ʢܴ���
��b��0���ʢ���ȷ��
��ͼ����y��Ľ�����y����ϰ��ᣬ
��c��0��
��abc��0���ʢ���ȷ��
����ȷ����4����
��ѡB��
�����͡���ѡ��
��������
10
����Ŀ����ͼ���ڡ�ABC�У���B����C��36�㣬AB�Ĵ�ֱƽ���߽�BC�ڵ�D����AB�ڵ�H��AC�Ĵ�ֱƽ���߽�BC�ڵ�E����AC�ڵ�G������AD��AE�������н��۴������( )

A. ![]() B. AD��AE����BAC���ȷ�
B. AD��AE����BAC���ȷ�
C. ��ABE�ա�ACD D. S��ADH��S��CEG
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���۵������ε�һ��AD��ʹ��D����BC���ϵĵ�F����BC=15��AB=9.
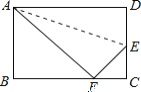
��1��FC�ij�����2��EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ���Ŀ������������ij��ѧ��ȫУ��Χ�������ȡ����ѧ�������ʾ�����. �ʾ�����ѧ��ѡ����ϲ���Ŀ����������ࣨÿ��ֻѡһ�ࣩ��ѡ���������ࡢ�����ࡢ�����༰���������࣬��������ݻ��Ƴ�����ͳ��ͼ������ͳ��ͼ����ͼ��ʾ��.
��1��������ռ�İٷֱ���_______,ѡ��������������________
��2�����ʾ������У�С����С��ֱ�ѡ����������������࣬Уѧ����Ҫ��ѡ����������������ѧ���зֱ��ȡһ��ѧ���μӻ�����б�����״ͼ�ķ�����С����С��ǡ�ö���ѡ�еĸ��ʣ�
��3�������ѧУ��500��ѧ����������Ƹ�ѧУ����ϲ�������˶���ѧ��Լ�ж�������
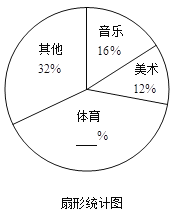
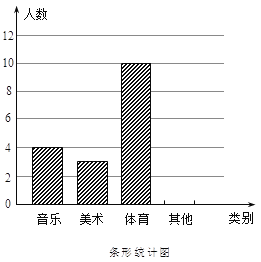
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com