
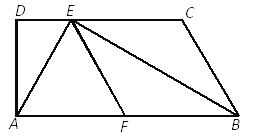
【题目】如图,已知梯形ABCD中,AB∥CD,∠D=90°,BE平分∠ABC,交CD于点E,F是AB的中点,联结AE、EF,且AE⊥BE.
求证:(1)四边形BCEF是菱形;
(2)![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】分析:(1)根据角平分线的性质可得出∠ABE=∠CBE,由直角三角形斜边上中线等于斜边的一半可得出EF=BF=![]() AB,进而可得出∠FEB=∠FBE=∠CBE,由“内错角相等,两直线平行”可得出EF∥BC,结合AB∥CD可得出四边形BCEF是平行四边形,再由邻边EF=BF即可证出四边形BCEF是菱形;
AB,进而可得出∠FEB=∠FBE=∠CBE,由“内错角相等,两直线平行”可得出EF∥BC,结合AB∥CD可得出四边形BCEF是平行四边形,再由邻边EF=BF即可证出四边形BCEF是菱形;
(2)根据菱形的性质可得出BC=BF,结合BF=![]() AB可得出AB=2BC,由AB∥CD可得出∠DEA=∠EAB,结合∠D=∠AEB=90°可证出△EDA∽△AEB,根据相似三角形的性质可得出BEAE=ADBA,代入BA=2BC即可证出结论.
AB可得出AB=2BC,由AB∥CD可得出∠DEA=∠EAB,结合∠D=∠AEB=90°可证出△EDA∽△AEB,根据相似三角形的性质可得出BEAE=ADBA,代入BA=2BC即可证出结论.
详解:(1)∵BE平分∠ABC,∴∠ABE=∠CBE.
∵AE⊥BE,∴∠AEB=90°.
∵F是AB的中点,∴EF=BF=![]() AB,∴∠FEB=∠FBE=∠CBE,∴EF∥BC.
AB,∴∠FEB=∠FBE=∠CBE,∴EF∥BC.
∵AB∥CD,∴四边形BCEF是平行四边形.
∵EF=BF,∴四边形BCEF是菱形.
(2)∵四边形BCEF是菱形,∴BC=BF.
∵BF=![]() AB,∴AB=2BC.
AB,∴AB=2BC.
∵AB∥CD,∴∠DEA=∠EAB.
∵∠D=∠AEB=90°,∴△EDA∽△AEB,∴![]() =
=![]() ,∴BEAE=ADBA,∴BEAE=2ADBC.
,∴BEAE=ADBA,∴BEAE=2ADBC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
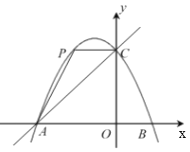
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
(1)求抛物线的表达式;
(2)如图,当CP//AO时,求∠PAC的正切值;
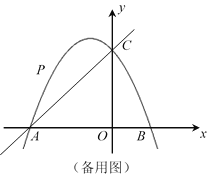
(3)当以AP、AO为邻边的平行四边形第四个顶点恰好也在抛物线上时,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的5×5的正方形网格中,每个小正方形的边长均为1,按下列要求画图或填空;

(1)画一条线段AB使它的另一端点B落在格点上(即小正方形的顶点),且AB=2![]() ;
;
(2)以(1)中的AB为边画一个等腰△ABC,使点C落在格点上,且另两边的长都是无理数;
(3)△ABC的周长为 ,面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
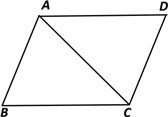
【题目】如图,已知平行四边形ABCD中,AC=BC,∠ACB=45°,将三角形ABC沿着AC翻折,点B落在点E处,联结DE,那么![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC 中,∠ACB=90°,BC=2,AC=3,以点C为圆心、CB为半径的圆交AB于点D,过点A作AE∥CD,交BC延长线于点E.
(1)求CE的长;
(2)P是 CE延长线上一点,直线AP、CD交于点Q.
①如果△ACQ ∽△CPQ,求CP的长;
②如果以点A为圆心,AQ为半径的圆与⊙C相切,求CP的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
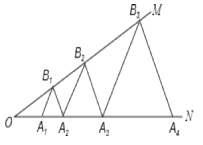
【题目】如图,已知:∠MON=30°,点A![]() 、A
、A![]() 、A
、A![]() …在射线ON上,点B
…在射线ON上,点B![]() 、B
、B![]() 、B
、B![]() …在射线OM上,△A
…在射线OM上,△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() …均为等边三角形,若OA
…均为等边三角形,若OA![]() =1,则△A
=1,则△A![]() B
B![]() A
A![]() 的边长为____
的边长为____
查看答案和解析>>
科目:初中数学 来源: 题型:
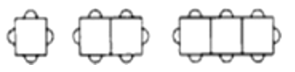
【题目】按下图方式摆放餐桌和椅子,
 …
…
(1)1张长方形餐桌可坐4人,2张长方形餐桌拼在一起可坐______人.
(2)按照上图的方式继续排列餐桌,完成下表.
桌子张数 | 3 | 4 | 5 | n |
可坐人数 | ______ | ______ | ______ | ______ |
(3)一家餐厅有40张这样的长方形餐桌,某用餐单位要求餐厅按照上图方式,每8张长方形餐桌拼成1张大桌子,则该餐厅此时能容纳多少人用餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
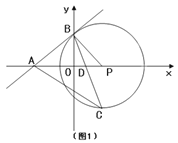
【题目】如图1,点A、B、P分别在两坐标轴上,∠APB=60°,PB=m,PA=2m,以点P为圆心、PB为半径作⊙P,作∠OBP的平分线分别交⊙P、OP于C、D,连接AC.
(1)求证:直线AB是⊙P的切线.
(2)设△ACD的面积为S,求S关于m的函数关系式.
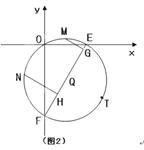
(3)如图2,当m=2时,把点C向右平移一个单位得到点T,过O、T两点作⊙Q交x轴、y轴于E、F两点,若M、N分别为两弧![]() 的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
的中点,作MG⊥EF,NH⊥EF,垂足为G、H,试求MG+NH的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com