练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在如图所示的5×5的正方形网格中，每个小正方形的边长均为1，按下列要求画图或填空；

    （1）画一条线段AB使它的另一端点B落在格点上（即小正方形的顶点），且AB=2；

    （2）以（1）中的AB为边画一个等腰△ABC，使点C落在格点上，且另两边的长都是无理数；

    （3）△ABC的周长为　　　　　　，面积为　　　　　　．

    【答案】（1）见解析；（2）见解析；（3），4.

    【解析】

    （1）直接利用勾股定理得出B点位置；
    （2）利用勾股定理结合等腰三角形的性质得出答案；
    （3）直接利用勾股定理以及三角形面积求法得出答案．

    解：（1）如图所示：AB即为所求；

    （2）如图所示：△ABC即为所求；

    （3）周长为：2++=2（+），
    面积为：9-×1×3-×2×2-×1×3=4．
    故答案为：2（+），4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某市举行知识大赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．

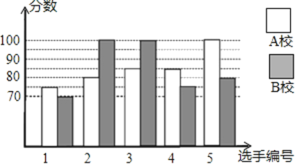
    （1）根据图示填写下表：

    （2）结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好；

    （3）计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解不等式（组）：

    （Ⅰ）解不等式：＜

    （Ⅱ）解不等式组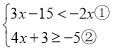

    请结合题意填空，完成本题的解答；

    （1）解不等式①，得：　 　；

    （2）解不等式②，得：　 　；

    （3）把不等式①和②的解集在如图数轴上表示出来；

    （4）原不等式组的解集为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，添加一个条件，仍不能证明四边形BECF为正方形的是

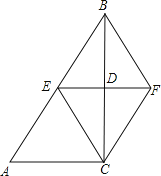
    A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

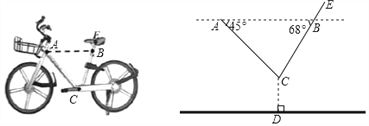
    【题目】如图，一辆摩拜单车放在水平的地面上，车把头下方A处与坐垫下方B处在平行于地面的水平线上，A、B之间的距离约为49cm，现测得AC、BC与AB的夹角分别为45°与68°，若点C到地面的距离CD为28cm，坐垫中轴E处与点B的距离BE为4cm，求点E到地面的距离（结果保留一位小数）．（参考数据：sin68°≈0.93，cos68°≈0.37，cot68°≈0.40）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

    （1）求证：AF=DC；

    （2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知梯形ABCD中，AB∥CD，∠D=90°，BE平分∠ABC，交CD于点E，F是AB的中点，联结AE、EF，且AE⊥BE．

    求证：（1）四边形BCEF是菱形；

    （2）.

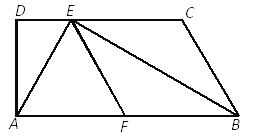
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：若线段上的一个点把这条线段分成1：2的两条线段，则称这个点是这条线段的三等分点．如图1，点C在线段AB上，且AC：CB＝1：2，则点C是线段AB的一个三等分点，显然，一条线段的三等分点有两个．

    （1）已知：如图2，DE＝15cm，点P是DE的三等分点，求DP的长．

    （2）已知，线段AB＝15cm，如图3，点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动；点Q从点B出发，先向点A方向运动，当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm，设运动时间为t秒．

    ①若点P点Q同时出发，且当点P与点Q重合时，求t的值．

    ②若点P点Q同时出发，且当点P是线段AQ的三等分点时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中,规定：抛物线y=a(xh) +k的关联直线为y=a(xh)+k.

    例如：抛物线y=2(x+1) 3的关联直线为y=2(x+1)3，即y=2x1.

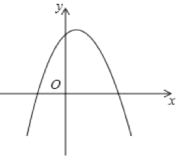
    (1)如图,对于抛物线y=(x1) +3.

    ①该抛物线的顶点坐标为___，关联直线为___，该抛物线与其关联直线的交点坐标为___和___；

    ②点P是抛物线y=(x1) +3上一点,过点P的直线PQ垂直于x轴,交抛物线y=(x1) +3的关联直线于点Q.设点P的横坐标为m,线段PQ的长度为d(d>0)，求当d随m的增大而减小时，d与m之间的函数关系式，并写出自变量m的取值范围。

    (2)顶点在第一象限的抛物线y=a(x1) +4a与其关联直线交于点A,B(点A在点B的左侧)，与x轴负半轴交于点C，直线AB与x轴交于点D，连结AC、BC.

    ①求△BCD的面积(用含a的代数式表示).

    ②当△ABC为钝角三角形时，直接写出a的取值范围。

    查看答案和解析>>

    同步练习册答案