
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
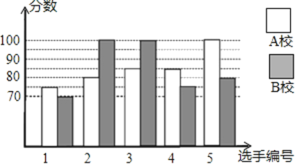
(1)根据图示填写下表:

(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
【答案】(1)见解析;(2)A校成绩好些;(3)A校代表队选手成绩较为稳定.
【解析】
(1)根据平均数、众数、中位数的概念以及求解方法分别进行计算补全统计表即可;
(2)根据平均数和中位数的统计意义分析得出即可;
(3)分别求出A校、B校的方差进而进行判断即可.
(1)A校平均数为:![]() ×(75+80+85+85+100)=85,众数85;
×(75+80+85+85+100)=85,众数85;
B校成绩按从小到大排序为:70、75、80、100、100,所以中位数为80,
填表如下:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | 85 | 85 | 85 |
B校 | 85 | 80 | 100 |
故答案为:85;85;80;
(2)A校成绩好些.因为两个队的平均数都相同,A校的中位数高,
所以在平均数相同的情况下中位数高的A校成绩好些;
(3)∵A校的方差
s12=![]() ×[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,
×[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,
B校的方差
s22=![]() ×[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160,
×[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160,
∴s12<s22,
因此,A校代表队选手成绩较为稳定.


科目:初中数学 来源: 题型:
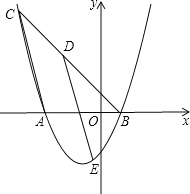
【题目】如图,已知抛物线y=![]() x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
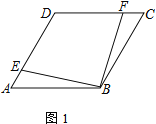
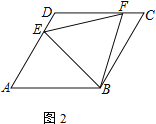
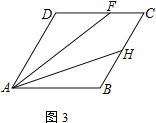
【题目】四边形ABCD为菱形,点E在边AD上,点F在边CD上
(1) 若AE=CF,求证:EB=BF
(2) 若AD=4,DE=CF,且△EFB为等边三角形,求四边形DEBF的面积
(3) 若∠DAB=60°,点H在边BC上,且BH=HC=2.若∠DFA=2∠HAB,直接写出CF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1的圆O1与半径为3的圆O2相内切,如果半径为2的圆与圆O1和圆O2都相切,那么这样的圆的个数是 ( )
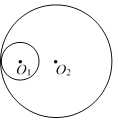
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块矩形纸片ABCD,AB=8,AD=6.将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则CF的长为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识背景)在学习计算框图时,可以用![]() 表示数据输入、输出框;
表示数据输入、输出框;![]() 用表示数据处理和运算框:用◇表示数据判断框(根据条件决定执行两条路径中的某一条)
用表示数据处理和运算框:用◇表示数据判断框(根据条件决定执行两条路径中的某一条)
(尝试解决)
(1)①如图1,当输入数![]() 时,输出数y=_________;
时,输出数y=_________;
②如图2,第一个“![]() ”内,应填_________;第二个“
”内,应填_________;第二个“![]() ”内,应填_________;
”内,应填_________;
(2)①如图3,当输入数![]() 时,输出数
时,输出数![]() =_________;
=_________;
②如图4,当输出的值![]() =26,则输入的值
=26,则输入的值![]() =_________;
=_________;
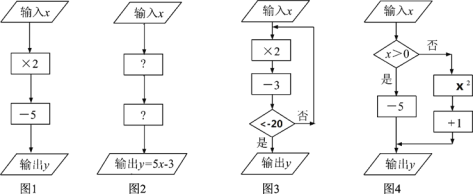
(实际应用)
(3)为鼓励节约用水,决定对用水实行“阶梯价”:当每月用水量不超过10吨时(含10吨),以3元/吨的价格收费;当每月用水量超过10吨时,超过部分以4元/吨的价格收费.请设计出一个“计算框图”,使得输入数为用水量![]() ,输出数为水费
,输出数为水费![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
(1)求抛物线的表达式;
(2)如图,当CP//AO时,求∠PAC的正切值;
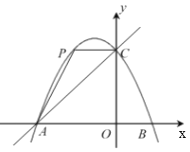
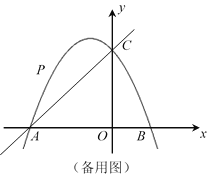
(3)当以AP、AO为邻边的平行四边形第四个顶点恰好也在抛物线上时,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级共有800名学生,准备调查他们对“低碳”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查七年级部分女生;
方案二:调查七年级部分男生;
方案三:到七年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是 ;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;

(3)在扇形统计图中,“比较了解”所在扇形的圆心角的度数是 .
(4)请你估计该校七年级约有 名学生比较了解“低碳”知识.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的5×5的正方形网格中,每个小正方形的边长均为1,按下列要求画图或填空;

(1)画一条线段AB使它的另一端点B落在格点上(即小正方形的顶点),且AB=2![]() ;
;
(2)以(1)中的AB为边画一个等腰△ABC,使点C落在格点上,且另两边的长都是无理数;
(3)△ABC的周长为 ,面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com