
����Ŀ��ijУ���꼶����800��ѧ�������������Ƕ�����̼��֪ʶ���˽�̶ȣ�
��1����ȷ�����鷽ʽʱ����ί������������ַ�����
����һ���������꼶����Ů����
���������������꼶����������
�������������꼶ÿ����ȥ�������һ��������ѧ����
������������д����Ե�һ���������� ����
��2����ί����������д����Եĵ��鷽���������ռ��������ݻ��Ƴ�������������ͳ��ͼ����ͼ�١�ͼ����ʾ�����������ͼ����Ϣ��������ͳ��ͼ����������

��3��������ͳ��ͼ�У����Ƚ��˽����������ε�Բ�ĽǵĶ������� ����
��4��������Ƹ�У���꼶Լ���� ����ѧ���Ƚ��˽�����̼��֪ʶ��
���𰸡���1��������2������������3��108 ����4��240.
�������������������1������ѧ�������Ƚ϶࣬���ó������鷽ʽ������һ��������ֻ�漰��������Ů��һ�����棬����Ƭ�棬����Ӧѡ����������2����Ϊ���˽�Ϊ5�ˣ���ռ�ٷֱ�Ϊ10%�����Ե�������Ϊ50�ˣ��Ƚ��˽�Ϊ15�ˣ�����ռ�ٷֱ�Ϊ30%����ô�˽�һ�����ռ�ٷֱ���60%������Ϊ30�ˣ���ȫͳ��ͼ���ɣ���3����360����ԡ��Ƚ��˽⡱��ռ�ٷֱȼ����������4�������������ԡ��Ƚ��˽⡱��ռ�ٷֱȼ�����⣮
���������
��1������һ��������ֻ�漰��������Ů��һ�����棬����Ƭ�棬��Ӧѡ��������
��2����������ã�5��10%=50���ˣ���
�˽�һ��������ǣ�50��5��15=30���ˣ���
�˽�һ���������ռ�İٷֱ��ǣ�![]() ��100%=60%��
��100%=60%��
�Ƚ��˽����ռ�İٷ��ǣ�1��60%��10%=30%��
��ͼ���£�
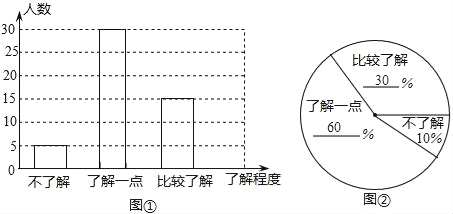
��3�����Ƚ��˽����������ε�Բ�ĽǵĶ�����360���30%=108�㣻
��4����������ã�800��30%=240������.
�𣺸�У���꼶Լ��240��ѧ���Ƚ��˽�����̼��֪ʶ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
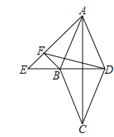
����Ŀ����ͼ����E������ABCD�ĶԽ���DB���ӳ����ϣ��ҡ�AED=45������B��AE�Ĵ��߽�AE��F������FD������AFD=60��ʱ��![]() =___________
=___________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о���֪ʶ������AУ��BУ���ɳ�5��ѡ����ɴ����ӲμӾ�������У�ɳ�ѡ�ֵľ����ɼ���ͼ��ʾ��
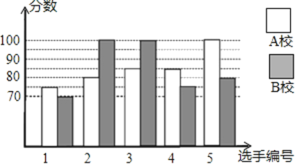
��1������ͼʾ��д�±���

��2�������У�ɼ���ƽ��������λ���������ĸ�ѧУ�ľ����ɼ��Ϻã�
��3��������У�����ɼ��ķ�����ж��ĸ�ѧУ������ѡ�ֳɼ���Ϊ�ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
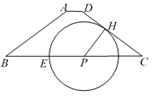
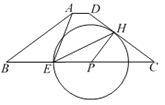
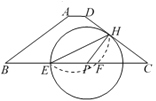
����Ŀ����ͼ��������ABCD�У�AD//BC��AB=DC=5��AD=1��BC=9����PΪ��BC��һ���㣬��PH��DC������H�ڱ�DC�ϣ��Ե�PΪԲ��PHΪ�뾶��Բ��������PB�ڵ�E.
��1����ԲP����Aʱ����ԲP�İ뾶��
��2���ֱ�����EH��EA������ABE�ס�CEHʱ���Ե�BΪԲ�ģ�rΪ�뾶��ԲB��ԲP�ཻ������ԲB�İ뾶r��ȡֵ��Χ��
��3�����ӻ�![]() ��ֱ��EH���۽�BC�ڵ�F����ͨ������˵���߶�EH��EF�ı�ֵΪ��ֵ��������˶�ֵ.
��ֱ��EH���۽�BC�ڵ�F����ͨ������˵���߶�EH��EF�ı�ֵΪ��ֵ��������˶�ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������߶�AB=2����λ���ȣ���CD=4����λ���ȣ�����A�������ϱ�ʾ�����ǩ�8����C �������ϱ�ʾ������10�����߶�AB��6����λ����/����ٶ����������˶���ͬʱ�߶�CD��2����λ����/����ٶ�Ҳ���������˶���
![]()
��1���˶�t���B��ʾ������ ����C��ʾ������ ��(�ú���t�Ĵ���ʽ��ʾ)
��2�����˶��������BC=4����λ���ȣ���
��3��P���߶�AB��һ�㣬��B���˶����߶�CD��ʱ���Ƿ���ڹ�ϵʽ![]() �������ڣ����߶�PD�ij����������ڣ���˵�����ɣ�
�������ڣ����߶�PD�ij����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
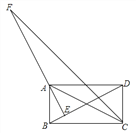
����Ŀ����ͼ������ABCD�У�AE��BD�ڵ�E��CFƽ�֡�BCD����EA���ӳ����ڵ�F����BC=4��CD=2���������н��ۣ��١�BAE=��CAD���ڡ�DBC=30�㣻��AE=![]() ����AF=
����AF=![]() ��������ȷ����______.����д������ȷ���۵���ţ�
��������ȷ����______.����д������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ���飩��
���ⲻ��ʽ��![]() ��
��![]()
���ⲻ��ʽ��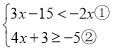
����������գ���ɱ���Ľ��
��1���ⲻ��ʽ�����ã��� ����
��2���ⲻ��ʽ�����ã��� ����
��3���Ѳ���ʽ�������Ľ⼯����ͼ�����ϱ�ʾ������
![]()
��4��ԭ����ʽ��Ľ⼯Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=90�㣬BC�Ĵ�ֱƽ����EF��BC�ڵ�D����AB�ڵ�E����BE=BF������һ���������Բ���֤���ı���BECFΪ�����ε���
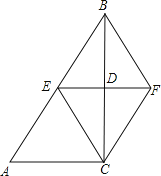
A. BC=AC B. CF��BF C. BD=DF D. AC=BF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���߶��ϵ�һ����������߶ηֳ�1��2�������߶Σ����������������߶ε����ȷֵ㣮��ͼ1����C���߶�AB�ϣ���AC��CB��1��2�����C���߶�AB��һ�����ȷֵ㣬��Ȼ��һ���߶ε����ȷֵ���������
��1����֪����ͼ2��DE��15cm����P��DE�����ȷֵ㣬��DP�ij���
��2����֪���߶�AB��15cm����ͼ3����P�ӵ�A������ÿ��1cm���ٶ�������AB�����B�����˶�����Q�ӵ�B�����������A�����˶��������P�غϺ������ı䷽�����Pͬ��������ٶ�ʼ��Ϊÿ��2cm�����˶�ʱ��Ϊt�룮
������P��Qͬʱ�������ҵ���P���Q�غ�ʱ����t��ֵ��
������P��Qͬʱ�������ҵ���P���߶�AQ�����ȷֵ�ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com