
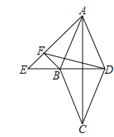
【题目】如图,点E在菱形ABCD的对角线DB的延长线上,且∠AED=45°,过B作AE的垂线交AE于F,连接FD.当∠AFD=60°时,![]() =___________
=___________
【答案】![]()
【解析】
首先作辅助线,延长FB交AC于点G,连接DG,因为∠AED=45°,BF⊥AE,得出∠EBF=45°,又因为菱形ABCD,得出∠GBD=∠GDB=∠EBF=45°,进而得出∠BGD=90°,BG=GD,又因为∠AFD=60°,得出∠DFG=30°,在Rt△FGD中,设BG=GD=x,FB+根据三角函数性质可得BG=![]() GD,进而得出FB=
GD,进而得出FB=![]() ,又△FEB∽△GDB,可得出
,又△FEB∽△GDB,可得出 ,即可得解.
,即可得解.
解:
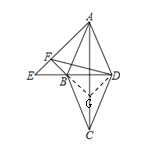
如图,延长FB交AC于点G,连接DG
∵∠AED=45°,BF⊥AE
∴∠EBF=45°
∵菱形ABCD,
∴∠GBD=∠GDB=∠EBF=45°
∴∠BGD=90°,BG=GD,
又∵∠AFD=60°
∴∠DFG=30°
在Rt△FGD中,设BG=GD=x
FB+BG=![]() GD
GD
∴FB=![]()
又△FEB∽△GDB
∴
故答案为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
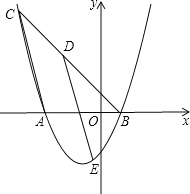
【题目】如图,已知抛物线y=![]() x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
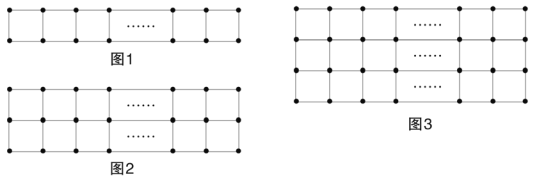
【题目】现有a枚棋子,按图1的方式摆放时刚好围成m个小正方形,按图2的方式摆放刚好围成2n个小正方形。
(1)用含m的代数式表示a,有a= ;用含n的代数式表示a,有a= ;
(2)若这a枚棋子按图3的方式摆放恰好围成3p个小正方形,
①P的值能取7吗?请说明理由;
②直接写出a的最小值:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】预习了“线段、射线、直线”一节的内容后,乐乐所在的小组,对如图展开了激烈的讨论,下列说法不正确的是( )
![]()
A. 直线AB与直线BA是同一条直线
B. 射线OA与射线AB是同一条射线
C. 射线OA与射线OB是同一条射线
D. 线段AB与线段BA是同一条线段
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.


(1)分别求出图①中线段AB、图②中抛物线所表示的函数表达式;
(2)当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
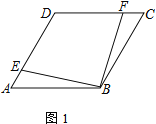
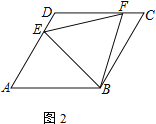
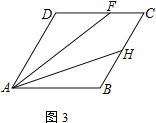
【题目】四边形ABCD为菱形,点E在边AD上,点F在边CD上
(1) 若AE=CF,求证:EB=BF
(2) 若AD=4,DE=CF,且△EFB为等边三角形,求四边形DEBF的面积
(3) 若∠DAB=60°,点H在边BC上,且BH=HC=2.若∠DFA=2∠HAB,直接写出CF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1的圆O1与半径为3的圆O2相内切,如果半径为2的圆与圆O1和圆O2都相切,那么这样的圆的个数是 ( )
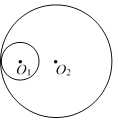
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级共有800名学生,准备调查他们对“低碳”知识的了解程度.
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查七年级部分女生;
方案二:调查七年级部分男生;
方案三:到七年级每个班去随机调查一定数量的学生.
请问其中最具有代表性的一个方案是 ;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将两个统计图补充完整;

(3)在扇形统计图中,“比较了解”所在扇形的圆心角的度数是 .
(4)请你估计该校七年级约有 名学生比较了解“低碳”知识.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com