
【题目】现有a枚棋子,按图1的方式摆放时刚好围成m个小正方形,按图2的方式摆放刚好围成2n个小正方形。
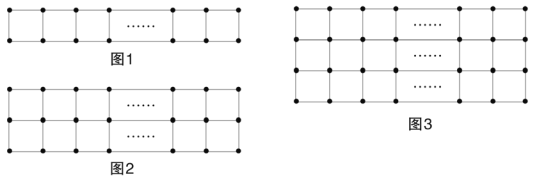
(1)用含m的代数式表示a,有a= ;用含n的代数式表示a,有a= ;
(2)若这a枚棋子按图3的方式摆放恰好围成3p个小正方形,
①P的值能取7吗?请说明理由;
②直接写出a的最小值:
【答案】(1)2m+2,3n+3;(2)①能,理由见解析;②8
【解析】
(1)根据图1每多一个正方形多用2枚棋子,写出摆放m个正方形所用的棋子的枚数;根据图2在两个小正方形的基础上,每多2个正方形多用3枚棋子,写出摆放2n个小正方形所用的棋子的枚数;
(2)①根据图3在三个小正方形的基础上,每多3个正方形多用4枚棋子,写出摆放3p个小正方形所用的棋子的枚数,当P的值取7时,可得出21个正方形共用32枚棋子;所以p可以取7;
②根据图3的摆放方式可得最少摆放三个正方形,可得出a的最小值
解:(1)由图可知,图1每多1个正方形,多用2枚棋子,
∴m个小正方形共用4+2(m-1)=2m+2枚棋子;
由图可知,图2两个小正方形的基础上,每多2个正方形多用3枚棋子,
∴2n个小正方形共用6+3(n-1)=3n+3 枚棋子;
故答案为:2m+2,3n+3;
(2)p可以取7
①根据图3在三个小正方形的基础上,每多3个正方形多用4枚棋子,
∴3p个小正方形共用8+4(p-1)=4p+4 枚棋子;
当p=7时,即21个正方形共用32枚棋子;
②根据图3的摆放方式可得最少摆放三个正方形,
∴a的最小值为:8
故答案为:8


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知线段a和线段AB ( a <AB).
![]()
(1)以AB为一边,画△ABC ,使AC a , A=50 ,用直尺、圆规作出△ABC边BC的垂直平分线,分别与边AB、BC 交于点D、E,联结CD ;(不写画法,保留作图痕迹)
(2)在(1)中,如果AB5 ,AC3 ,那么△ADC 的周长等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长.
(2)若C为线段AB上任意一点,满足AC+CB=a(cm),其他条件不变,你能猜想出MN的长度吗?并说明理由.
(3)若C在线段AB的延长线上,且满足AC-CB=b(cm),M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A﹣C﹣B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ的面积为y(cm2),y关于x的函数图象由C1,C2两段组成,如图2所示.
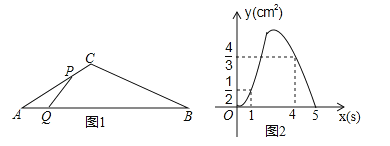
(1)求a的值;
(2)求图2中图象C2段的函数表达式;
(3)当点P运动到线段BC上某一段时△APQ的面积,大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
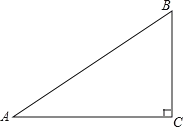
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
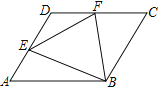
【题目】□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°.若AE=2,FC=3,则EF的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在菱形ABCD的对角线DB的延长线上,且∠AED=45°,过B作AE的垂线交AE于F,连接FD.当∠AFD=60°时,![]() =___________
=___________
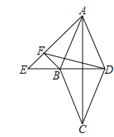
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题:
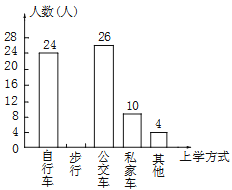
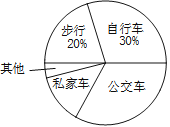
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(4)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
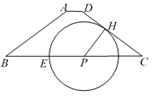
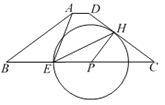
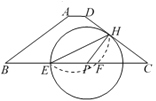
【题目】如图,在梯形ABCD中,AD//BC,AB=DC=5,AD=1,BC=9,点P为边BC上一动点,作PH⊥DC,垂足H在边DC上,以点P为圆心PH为半径画圆,交射线PB于点E.
(1)当圆P过点A时,求圆P的半径;
(2)分别联结EH和EA,当△ABE∽△CEH时,以点B为圆心,r为半径的圆B与圆P相交,试求圆B的半径r的取值范围;
(3)将劣弧![]() 沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值.
沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com