
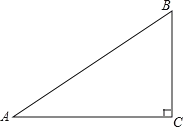
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B=_________.
【答案】![]() 或7
或7![]()
【解析】分析:分两种情况:①如图1,作辅助线,构建矩形,先由勾股定理求斜边AB=10,由中点的定义求出AD和BD的长,证明四边形HFGB是矩形,根据同角的三角函数列式可以求DG和DF的长,并由翻折的性质得:∠![]() =∠A,
=∠A, ![]() =AD=5,由矩形性质和勾股定理可以得出结论:
=AD=5,由矩形性质和勾股定理可以得出结论: ![]() =
=![]() ;②如图2,作辅助线,构建矩形
;②如图2,作辅助线,构建矩形![]() ,同理可以求出
,同理可以求出![]() 的长.
的长.
详解:分两种情况:
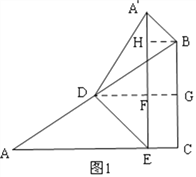
如图1,过D作DG⊥BC与G,交A′E与F,过B作BH⊥A′E与H,
∵D为AB的中点,
∴BD=![]() AB=AD,
AB=AD,
∵∠C=90,AC=8,BC=6,
∴AB=10,
∴BD=AD=5,
sin∠ABC=![]() ,
,
∴![]() ,
,
∴DG=4,
由翻折得:∠DA′E=∠A,A′D=AD=5,
∴sin∠DA′E=sin∠A=![]() ,
,
∴![]() ,
,
∴DF=3,
∴FG=43=1,
∵A′E⊥AC,BC⊥AC,
∴A′E∥BC,
∴∠HFG+∠DGB=180°,
∵∠DGB=90°,
∴∠HFG=90°,
∵∠EHB=90,
∴四边形HFGB是矩形,
∴BH=FG=1,
同理得:A′E=AE=81=7,
∴A′H=A′EEH=76=1,
在Rt△AHB中,由勾股定理得:A′B=![]() ;
;
②如图2,过D作MN∥AC,交BC与于N,过A′作A
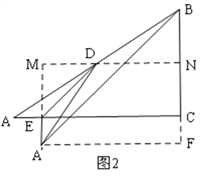
∵A′E⊥AC,
∴A′M⊥MN,A′E⊥A′F,
∴∠M=∠MA′F=90°,
∵∠ACB=90°,
∴∠F=∠ACB=90°,
∴四边形MA′FN是矩形,
∴MN=A′F,FN=A′M,
由翻折得:A′D=AD=5,
Rt△A′MD中,∴DM=3,A′M=4,
∴FN=A′M=4,
Rt△BDN中,∵BD=5,
∴DN=4,BN=3,
∴A′F=MN=DM+DN=3+4=7,
BF=BN+FN=3+4=7,
Rt△ABF中,由勾股定理得:A′B=![]() ;
;
综上所述![]() 的长为
的长为![]() 或
或![]()
故答案为: ![]() 或
或![]() .
.
本题考查的是图形的翻折变换及等腰直角三角形的性质、矩形的性质、平行线分线段成比例定理及勾股定理的综合运用,题型难度较大.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校抽查了某班级某月10天的用电量,数据如下表:
用电量/度 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是______度,中位数是______度;
(2)求这个班级平均每天的用电量;
(3)该校共有20个班级,该月共计30天,试估计该校该月总的用电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
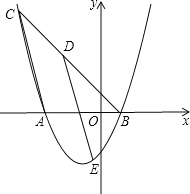
【题目】如图,已知抛物线y=![]() x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
x2+mx+n与x轴相交于点A、B两点,过点B的直线y=x+b交抛物线于另一点C(-5,6),点D是线段BC上的一个动点(点D与点B、C不重合),作DE∥AC,交该抛物线于点E,
(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在点D运动过程中,是否存在∠DEA=45°,若存在,则求此时线段AE的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有a枚棋子,按图1的方式摆放时刚好围成m个小正方形,按图2的方式摆放刚好围成2n个小正方形。
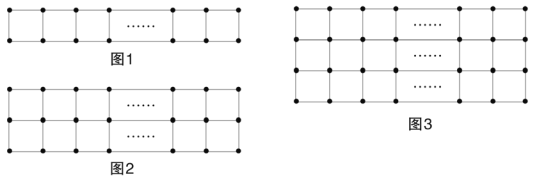
(1)用含m的代数式表示a,有a= ;用含n的代数式表示a,有a= ;
(2)若这a枚棋子按图3的方式摆放恰好围成3p个小正方形,
①P的值能取7吗?请说明理由;
②直接写出a的最小值:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】预习了“线段、射线、直线”一节的内容后,乐乐所在的小组,对如图展开了激烈的讨论,下列说法不正确的是( )
![]()
A. 直线AB与直线BA是同一条直线
B. 射线OA与射线AB是同一条射线
C. 射线OA与射线OB是同一条射线
D. 线段AB与线段BA是同一条线段
查看答案和解析>>
科目:初中数学 来源: 题型:
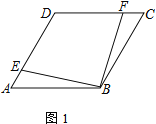
【题目】四边形ABCD为菱形,点E在边AD上,点F在边CD上
(1) 若AE=CF,求证:EB=BF
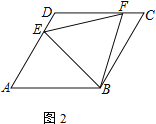
(2) 若AD=4,DE=CF,且△EFB为等边三角形,求四边形DEBF的面积
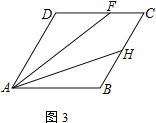
(3) 若∠DAB=60°,点H在边BC上,且BH=HC=2.若∠DFA=2∠HAB,直接写出CF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
(1)求抛物线的表达式;
(2)如图,当CP//AO时,求∠PAC的正切值;
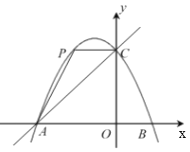
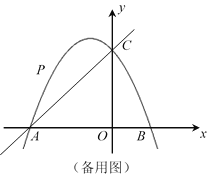
(3)当以AP、AO为邻边的平行四边形第四个顶点恰好也在抛物线上时,求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com