
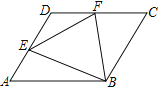
【题目】□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°.若AE=2,FC=3,则EF的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
【答案】A
【解析】
由DE=DF,AE=2,FC=3可知AB-BC=1,过点E作EM⊥AB于M,根据30°角所对的直角等于斜边的一半可得AM=1,进而得出BM=BC,将△BEM顺时针旋转120°得△BEN,连接FN,可证△BEF≌△BFN,即可得出EF=FN,过点N作NG⊥DC交DC的延长线于点G,利用勾股定理即可求出答案.
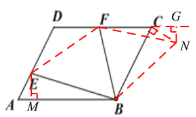
解:过点E作EM⊥AB于M,
在Rt△AEM中,∠A=60°,
∴∠AEM=30°,
∴AM=![]() AE=1,
AE=1,
∴ME=![]() ,
,
又∵DE=DF,AE=2,FC=3,
∴DC-AD=1,即AB-BC=1,
∴BM=BC,
将△BEM顺时针旋转120°得△BEN,连接FN,则CN=EM=![]() ,BE=BN,
,BE=BN,
∵∠EBF=60°,∠EBN=120°,
∴∠NBF=60°,
∴∠EBF=∠NBF
又∵BE=BN,BF=BF,
∴△BEF≌△BFN,
∴EF=FN,
过点N作NG⊥DC交DC的延长线于点G,
∵∠GCN=180°-60°-90°=30°,
∴NG=![]() NC=
NC=![]()
∴CG=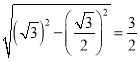
∴FG=3+![]() =
=![]()
∴FN=
∴EF=![]()
故答案为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
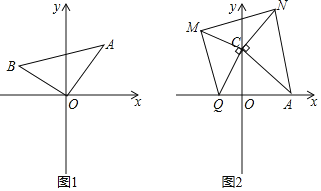
【题目】(1)如图1,等腰直角三角形![]() 的直角顶点
的直角顶点![]() 在坐标原点,点
在坐标原点,点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标.
的坐标.
(2)依据(1)的解题经验,请解决下面问题:
如图2,点![]() ,
,![]() 两点均在
两点均在![]() 轴上,且
轴上,且![]() ,分别以
,分别以![]() 为腰在第一、第二象限作等腰
为腰在第一、第二象限作等腰![]() ,
,![]() 连接
连接![]() ,与
,与![]() 轴交于点
轴交于点![]() 的长度是否发生改变?若不变,求
的长度是否发生改变?若不变,求![]() 的值;若变化,求
的值;若变化,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
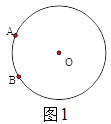
【题目】定义:数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.
理解:(1)如图![]() ,已知
,已知![]() 是⊙
是⊙![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
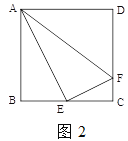
(2)如图![]() ,在正方形
,在正方形![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
运用:(3)如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,⊙
中,⊙![]() 的半径为
的半径为![]() ,点
,点![]() 是直线
是直线![]() 上的一点,若在⊙
上的一点,若在⊙![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,其面积的最小值为______.
为“智慧三角形”,其面积的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有a枚棋子,按图1的方式摆放时刚好围成m个小正方形,按图2的方式摆放刚好围成2n个小正方形。
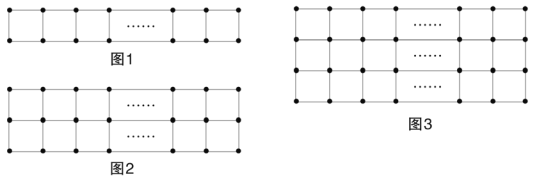
(1)用含m的代数式表示a,有a= ;用含n的代数式表示a,有a= ;
(2)若这a枚棋子按图3的方式摆放恰好围成3p个小正方形,
①P的值能取7吗?请说明理由;
②直接写出a的最小值:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲楼AB高20 m,乙楼CD高10 m,两栋楼之间的水平距离BD=20 m,小丽在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求电视塔的高度EF.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
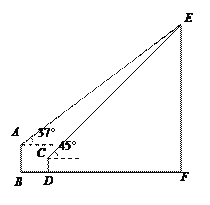
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.


(1)分别求出图①中线段AB、图②中抛物线所表示的函数表达式;
(2)当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区为治理污水,需要铺设一段全长为 720 米的污水排放管道.“…”.设原计划每天铺设 x 米,可以列出方程![]() ,根据情景及所列方程,题中用“…”表示的缺失条件应补为( )
,根据情景及所列方程,题中用“…”表示的缺失条件应补为( )
A.实际施工时每天的工作效率比原计划高 20%,结果提前 2 天完成任务;
B.原计划每天的工作效率比实际施工时低 20%,结果提前 2 天完成任务;
C.实际施工时每天的工作效率比原计划高 20%,结果延后 2 天完成任务;
D.原计划每天的工作效率比实际施工时低 20%,结果延后 2 天完成任务.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
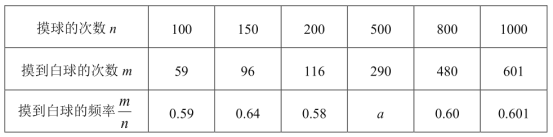
(1)上表中的a= ;
(2)“摸到白球”的概率的估计值是 (精确到0.1)
(3)试估算口袋中黑、白两种颜色的球各有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com