
【题目】在一只不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
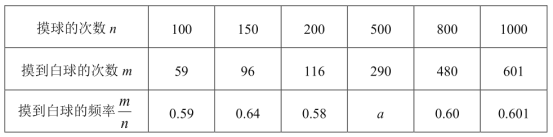
(1)上表中的a= ;
(2)“摸到白球”的概率的估计值是 (精确到0.1)
(3)试估算口袋中黑、白两种颜色的球各有多少个?
【答案】(1) 0.58;(2) 0.6;(3)白球12(个),黑球8 (个)
【解析】
(1)利用频率=频数÷样本容量直接求解即可;
(2)根据统计数据,当n很大时,摸到白球的频率接近0.60;
(3)根据利用频率估计概率,可估计摸到白球的概率为0.60,然后利用概率公式计算白球的个数.
(1)a=![]() =0.58,
=0.58,
故答案为:0.58;
(2)随着实验次数的增加“摸到白球”的频率趋向于0.60,所以其概率的估计值是0.60,
故答案为:0.60;
(3)由(2)摸到白球的概率估计值为0.60,
所以可估计口袋中白种颜色的球的个数=20×0.6=12(个),黑球2012=8(个).
答:黑球8个,白球12个.


科目:初中数学 来源: 题型:
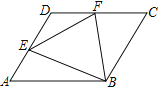
【题目】□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°.若AE=2,FC=3,则EF的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学测验后,王老师把某一小组10名同学的成绩以平均成绩为基准,并以高于平均成绩记为“+”,分别记为+10分,-5分,0分,+8分,-3分,+6分,-5分,-3分,+4分,-12分,通过计算知道这10名同学的平均成绩是82分.
(1)这一小组成绩最高分与最低分相差多少分?
(2)如果成绩不低于80分为优秀,那么这10名同学在这次数学测验中优秀率是百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则: 若n=24,则第100次“F”运算的结果是________.
若n=24,则第100次“F”运算的结果是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
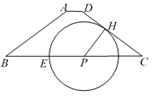
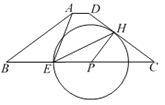
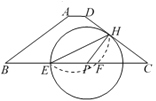
【题目】如图,在梯形ABCD中,AD//BC,AB=DC=5,AD=1,BC=9,点P为边BC上一动点,作PH⊥DC,垂足H在边DC上,以点P为圆心PH为半径画圆,交射线PB于点E.
(1)当圆P过点A时,求圆P的半径;
(2)分别联结EH和EA,当△ABE∽△CEH时,以点B为圆心,r为半径的圆B与圆P相交,试求圆B的半径r的取值范围;
(3)将劣弧![]() 沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值.
沿直线EH翻折交BC于点F,试通过计算说明线段EH和EF的比值为定值,并求出此定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上出了一道解方程的题:![]() ,小明马上举起了手,要求到黑板上去做,他是这样做的:4(2x﹣1)=1﹣3(x+2),①
,小明马上举起了手,要求到黑板上去做,他是这样做的:4(2x﹣1)=1﹣3(x+2),①
8x﹣4=1﹣3x﹣6,②
8x+3x=1﹣6+4,③
11x=﹣1,④
x=﹣![]() .⑤
.⑤
老师说:小明解一元一次方程的一般步骤都掌握了,但解题时有一步做错了.请你指出他错在第 步(填编号),然后再细心地解下面的方程,相信你一定能做对.
(1)5(x+8)=6(2x﹣7)+5;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
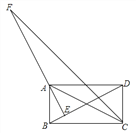
【题目】如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=![]() ;④AF=
;④AF=![]() ,其中正确的是______.(填写所有正确结论的序号)
,其中正确的是______.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
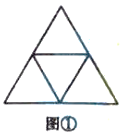
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有![]() 个;
个;
边长为2的正三角形一共有1个.
探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有![]() 个;边长为2的正三角形共有
个;边长为2的正三角形共有![]() 个.
个.

探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鹿山广场元旦期间搞促销活动,如图.

(1)小哲在促销活动时两次购物分别用了135元和481元.
①若小哲购物时没有促销活动,则他共需付多少钱?
②若你需购这些同样的物品,请问还有更便宜的购物方案吗?若有,请说出购物方案,并算出共需付多少钱;若没有,则说明理由.
(2)若小明购了原价为a元的物品,小红购了原价为b元的物品,且a<b,但最后小明所付的钱反而比小红多.
①你列举一对a,b的值;
②求符合条件的整数a,b共有几对?(直接答案即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com