
【题目】某区为治理污水,需要铺设一段全长为 720 米的污水排放管道.“…”.设原计划每天铺设 x 米,可以列出方程![]() ,根据情景及所列方程,题中用“…”表示的缺失条件应补为( )
,根据情景及所列方程,题中用“…”表示的缺失条件应补为( )
A.实际施工时每天的工作效率比原计划高 20%,结果提前 2 天完成任务;
B.原计划每天的工作效率比实际施工时低 20%,结果提前 2 天完成任务;
C.实际施工时每天的工作效率比原计划高 20%,结果延后 2 天完成任务;
D.原计划每天的工作效率比实际施工时低 20%,结果延后 2 天完成任务.
科目:初中数学 来源: 题型:
【题目】已知数轴上的A、B两点分别对应数字a、b,且a、b满足|4a-b|+(a-4)2=0
![]()
(1)a= ,b= ,并在数轴上面出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和点Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P点到达C点后,再立刻以同样的速度返回,运动到终点A.求点P和点Q运动多少秒时,P、Q两点之间的距离为4,并求此时点Q对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
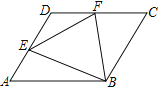
【题目】□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°.若AE=2,FC=3,则EF的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在上学的路上要经过多个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到信号灯是相互独立的.
(1).如果有2个路口,求小明在上学路上到第二个路口时第一次遇到红灯的概率.(请用“画树状图”或“列表”等方法写出分析过程)
(2).如果有n个路口,则小明在每个路口都没有遇到红灯的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题:
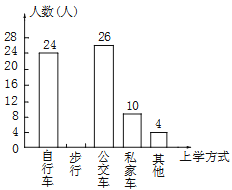
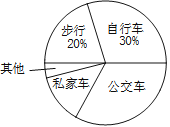
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(4)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将边长为 a 、b 的正方形 ABCD 按图 ① 中的比例进行分割,可以拼成一个长方形A1 B1C1D1 不重叠、无缝隙),如图②所示.
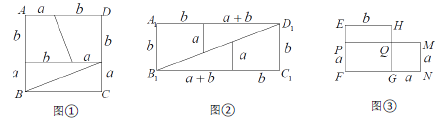
(1)根据图①可以拼成图②的面积关系,请写出 a 、b 之间存在的关系式;
(2)已知图③中,四边形 QMNG 与四边形EFGH 分别是以 a 、b 长为边的正方形与图①中的 a 、b 相同),在图 3 已有的四边形中,面积相等的四边形有几组?请分别写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学测验后,王老师把某一小组10名同学的成绩以平均成绩为基准,并以高于平均成绩记为“+”,分别记为+10分,-5分,0分,+8分,-3分,+6分,-5分,-3分,+4分,-12分,通过计算知道这10名同学的平均成绩是82分.
(1)这一小组成绩最高分与最低分相差多少分?
(2)如果成绩不低于80分为优秀,那么这10名同学在这次数学测验中优秀率是百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则: 若n=24,则第100次“F”运算的结果是________.
若n=24,则第100次“F”运算的结果是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
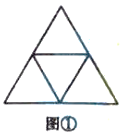
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有![]() 个;
个;
边长为2的正三角形一共有1个.
探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有![]() 个;边长为2的正三角形共有
个;边长为2的正三角形共有![]() 个.
个.

探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com