
����Ŀ����֪ʶ��������ѧϰ�����ͼʱ��������![]() ��ʾ�������롢�����
��ʾ�������롢�����![]() �ñ�ʾ���ݴ����������:�á��ʾ�����жϿ�(������������ִ������·���е�ijһ��)
�ñ�ʾ���ݴ����������:�á��ʾ�����жϿ�(������������ִ������·���е�ijһ��)
�����Խ����
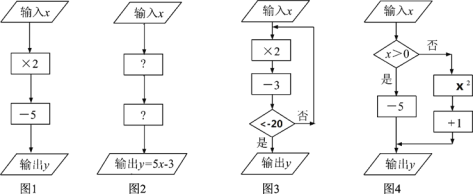
��1������ͼ1����������![]() ʱ�������y��_________��
ʱ�������y��_________��
����ͼ2����һ����![]() ���ڣ�Ӧ��_________���ڶ�����
���ڣ�Ӧ��_________���ڶ�����![]() ���ڣ�Ӧ��_________��
���ڣ�Ӧ��_________��
��2������ͼ3����������![]() ʱ�������
ʱ�������![]() ��_________��
��_________��
����ͼ4���������ֵ![]() ��26���������ֵ
��26���������ֵ![]() ��_________��
��_________��
��ʵ��Ӧ�ã�
��3��Ϊ������Լ��ˮ����������ˮʵ�������ݼ���:��ÿ����ˮ��������10��ʱ(��10��)����3Ԫ/�ֵļ۸��շѣ���ÿ����ˮ������10��ʱ������������4Ԫ/�ֵļ۸��շ�.����Ƴ�һ���������ͼ����ʹ��������Ϊ��ˮ��![]() �������Ϊˮ��
�������Ϊˮ��![]() .
.
���𰸡���1����-11������5��-3����2����-37����31��-5����3��������
��������
��1���ٰ�x=-3����ͼ1�еij����м���ȷ���������y���ɣ�
�ڸ�������Ĵ���ʽȷ����������Ӧ�������㼴�ɣ�
��2���ٰ�x=-2����ͼ3�еij����м���ȷ�������y���ɣ�
�ڰ�y=26����ͼ4�еij����м��㼴��ȷ��������x��ֵ��
��3����������ȷ������������ͼ���ɣ�
�⣺��1���ٰ�x=-3����ã�y=��-3����2-5=-6-5=-11��
�ڸ�������ã���һ����![]() ���ڣ�Ӧ���5���ڶ�����
���ڣ�Ӧ���5���ڶ�����![]() ���ڣ�Ӧ��-3��
���ڣ�Ӧ��-3��
��2���ٰ�x=-2����ã���-2����2-3=-4-3=-7��
��x=-7������-7����2-3=-14-3=-17��
��x=-17������-17����2-3=-34-3=-37��
��y=-37��
����x��0����y=26����ã�x=26+5=31��
��x��0����y=26����ã�x2+1=26����x=-5��
��x=31��-5��
��3����ͼ��ʾ��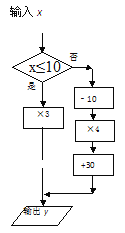



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABC�У���A=30�㣬��P�ӵ�A������2cm/s���ٶ�������A��C��B�˶�����Q�ӵ�A������a��cm/s�����ٶ���AB�˶���P��Q����ͬʱ��������ijһ���˶�����Bʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊx��s������APQ�����Ϊy��cm2����y����x�ĺ���ͼ����C1��C2������ɣ���ͼ2��ʾ��
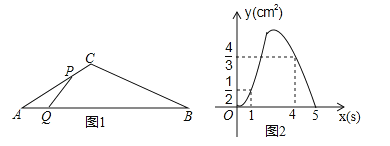
��1����a��ֵ��
��2����ͼ2��ͼ��C2�εĺ�������ʽ��
��3������P�˶����߶�BC��ijһ��ʱ��APQ����������ڵ���P���߶�AC������һ��ʱ��APQ���������x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˽�ȫУѧ����У��ѧ�ķ�ʽ����ȫУ�����ȡ��������ѧ�������ʾ����飮�ʾ�������������ѧ��ʽ��ѧ��ѡ��ÿ��ֻ��ѡһ��Ҳ��ܲ�ѡ��ͬʱ�ѵ���õ��Ľ�����Ƴ���ͼ��ʾ������ͳ��ͼ������ͳ��ͼ�������������������ͼ���ṩ����Ϣ����������⣺
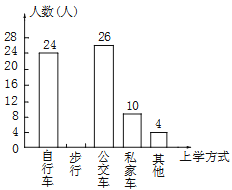
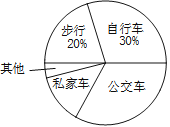
��1������ε����У�һ����ȡ�˶�����ѧ����
��2��ͨ�����㲹ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У�������������������Ӧ��Բ�Ľ��Ƕ��ٶȣ�
��4����ȫУ��1600��ѧ�������Ƹ�У����˽�ҳ���ѧ��ѧ��Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ѧ���������ʦ��ijһС��10��ͬѧ�ijɼ���ƽ���ɼ�Ϊ�������Ը���ƽ���ɼ���Ϊ��+�����ֱ��Ϊ+10�֣�-5�֣�0�֣�+8�֣�-3�֣�+6�֣�-5�֣�-3�֣�+4�֣�-12�֣�ͨ������֪����10��ͬѧ��ƽ���ɼ���82��.
��1����һС��ɼ���߷�����ͷ������ٷ�?
��2������ɼ�������80��Ϊ���㣬��ô��10��ͬѧ�������ѧ�������������ǰٷ�֮��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о���֪ʶ������AУ��BУ���ɳ�5��ѡ����ɴ����ӲμӾ�������У�ɳ�ѡ�ֵľ����ɼ���ͼ��ʾ��
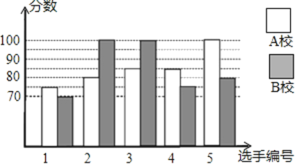
��1������ͼʾ��д�±���

��2�������У�ɼ���ƽ��������λ���������ĸ�ѧУ�ľ����ɼ��Ϻã�
��3��������У�����ɼ��ķ�����ж��ĸ�ѧУ������ѡ�ֳɼ���Ϊ�ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�ֶ�������n�ġ�F�����㣺�ٵ�nΪ����ʱ��F��n����3n+1���ڵ�nΪż��ʱ��F��n��![]() ������k��ʹF��n��Ϊ���������������������������㽻���ظ����У����磬ȡn��13����
������k��ʹF��n��Ϊ���������������������������㽻���ظ����У����磬ȡn��13���� ��n��24�����100�Ρ�F������Ľ����________��
��n��24�����100�Ρ�F������Ľ����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AD//BC��AB=DC=5��AD=1��BC=9����PΪ��BC��һ���㣬��PH��DC������H�ڱ�DC�ϣ��Ե�PΪԲ��PHΪ�뾶��Բ��������PB�ڵ�E.
��1����ԲP����Aʱ����ԲP�İ뾶��
��2���ֱ�����EH��EA������ABE�ס�CEHʱ���Ե�BΪԲ�ģ�rΪ�뾶��ԲB��ԲP�ཻ������ԲB�İ뾶r��ȡֵ��Χ��
��3�����ӻ�![]() ��ֱ��EH���۽�BC�ڵ�F����ͨ������˵���߶�EH��EF�ı�ֵΪ��ֵ��������˶�ֵ.
��ֱ��EH���۽�BC�ڵ�F����ͨ������˵���߶�EH��EF�ı�ֵΪ��ֵ��������˶�ֵ.
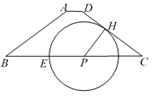
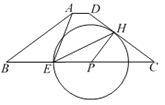
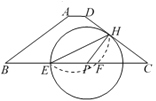
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AE��BD�ڵ�E��CFƽ�֡�BCD����EA���ӳ����ڵ�F����BC=4��CD=2���������н��ۣ��١�BAE=��CAD���ڡ�DBC=30�㣻��AE=![]() ����AF=
����AF=![]() ��������ȷ����______.����д������ȷ���۵���ţ�
��������ȷ����______.����д������ȷ���۵���ţ�
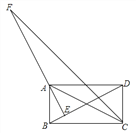
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��BC���ϵ����ߣ�E��AD���е㣬����A��BC��ƽ���߽�BE���ӳ����ڵ�F������CF��

��1����֤��AF=DC��
��2����AB��AC�����ж��ı���ADCF����״����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com