
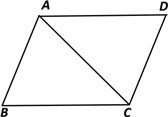
【题目】如图,已知平行四边形ABCD中,AC=BC,∠ACB=45°,将三角形ABC沿着AC翻折,点B落在点E处,联结DE,那么![]() 的值为________.
的值为________.
【答案】![]()
【解析】分析:依据△ACF和△DEF都是等腰直角三角形,设EF=DF=1,则DE=![]() ,设AF=CF=x,则AC=EC=1+x.在Rt△ACF中,依据AF2+CF2=AC2,可得x2+x2=(x+1)2,解得x=1+
,设AF=CF=x,则AC=EC=1+x.在Rt△ACF中,依据AF2+CF2=AC2,可得x2+x2=(x+1)2,解得x=1+![]() ,即可得到AC=2+
,即可得到AC=2+![]() ,进而得出
,进而得出![]() =
=![]() =
=![]() .
.
详解:如图,设AD与CE交于点F,由折叠可得,∠ACE=∠ACB=45°,而∠DAC=∠ACB=45°,∴∠AFC=90°,∠EFD=90°,AF=CF,由折叠可得,CE=AD,∴EF=DF,∴△ACF和△DEF都是等腰直角三角形,设EF=DF=1,则DE=![]() ,设AF=CF=x,则AC=EC=1+x.∵Rt△ACF中,AF2+CF2=AC2,∴x2+x2=(x+1)2,解得:x=1+
,设AF=CF=x,则AC=EC=1+x.∵Rt△ACF中,AF2+CF2=AC2,∴x2+x2=(x+1)2,解得:x=1+![]() 或x=1﹣
或x=1﹣![]() (舍去),∴AC=2+
(舍去),∴AC=2+![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
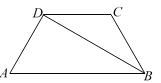
【题目】已知:如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
求:(1)求∠CDB的度数;
(2)当AD=2时,求对角线BD的长和梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
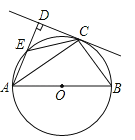
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
(1)求证:CE=CB;
(2)若AC=![]() ,CE=
,CE=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
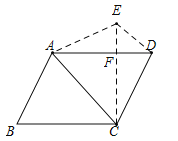
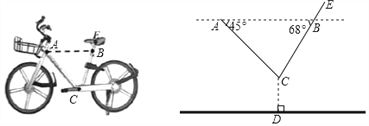
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实数a,b,c在数轴上的位置如图所示,则下列式子中一定成立的是( )
![]()
A.|a﹣b|=a+bB.|a+c|=a+c
C.|b+c|=﹣b﹣cD.|a+b﹣c|=﹣a﹣b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
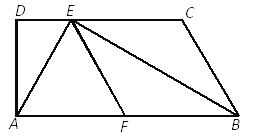
【题目】如图,已知梯形ABCD中,AB∥CD,∠D=90°,BE平分∠ABC,交CD于点E,F是AB的中点,联结AE、EF,且AE⊥BE.
求证:(1)四边形BCEF是菱形;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数大致图象是( )
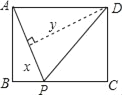
A. 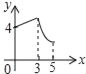 B.
B. 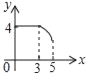 C.
C. 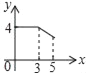 D.
D. 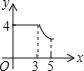
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是最大的负整数,且
是最大的负整数,且![]() 、b、c满足(c﹣5)2+|
、b、c满足(c﹣5)2+|![]() +b|=0,请回答问题.
+b|=0,请回答问题.
![]()
(1)请直接写出![]() 、b、c的值:
、b、c的值:![]() = ,b= ,c= .
= ,b= ,c= .
(2)![]() 、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0 ≤ x ≤ 1时),请化简式子:|x+1|﹣|x﹣1|+2|x-5|(请写出化简过程).
、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0 ≤ x ≤ 1时),请化简式子:|x+1|﹣|x﹣1|+2|x-5|(请写出化简过程).
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和8个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:c=10,且a,b满足(a+26)2+|b+c|=0,请回答问题:
(1)请直接写出a,b,c的值:a= ,b= ;
(2)在数轴上a、b、c所对应的点分别为A、B、C,记A、B两点间的距离为AB,则AB= ,AC= ;
(3)在(1)(2)的条件下,若点M从点A出发,以每秒1个单位长度的速度向右运动,当点M到达点C时,点M停止;当点M运动到点B时,点N从点A出发,以每秒3个单位长度向右运动,点N到达点C后,再立即以同样的速度返回,当点N到达点A时,点N停止.从点M开始运动时起,至点M、N均停止运动为止,设时间为t秒,请用含t的代数式表示M,N两点间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com