
【题目】已知:![]() 是最大的负整数,且
是最大的负整数,且![]() 、b、c满足(c﹣5)2+|
、b、c满足(c﹣5)2+|![]() +b|=0,请回答问题.
+b|=0,请回答问题.
![]()
(1)请直接写出![]() 、b、c的值:
、b、c的值:![]() = ,b= ,c= .
= ,b= ,c= .
(2)![]() 、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0 ≤ x ≤ 1时),请化简式子:|x+1|﹣|x﹣1|+2|x-5|(请写出化简过程).
、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0 ≤ x ≤ 1时),请化简式子:|x+1|﹣|x﹣1|+2|x-5|(请写出化简过程).
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和8个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
【答案】(1)![]() =﹣1,b=1,c=5;(2)10;(3)不变,2.
=﹣1,b=1,c=5;(2)10;(3)不变,2.
【解析】
(1)根据绝对值和完全平方式的非负性求值即可;(2)由0 ≤ x ≤ 1得出x+1>0; x﹣1≤0;x-5![]() 0,然后根据绝对值的意义进行化简;(3)分别表示出t秒后,点A,B,C所表示的数,然后根据两点间的距离求得BC,AB的长度,然后进行计算并化简.
0,然后根据绝对值的意义进行化简;(3)分别表示出t秒后,点A,B,C所表示的数,然后根据两点间的距离求得BC,AB的长度,然后进行计算并化简.
解:(1)∵![]() 是最大的负整数,
是最大的负整数,
∴![]() =﹣1
=﹣1
∵(c﹣5)2+|![]() +b|=0
+b|=0
∴c-5=0;a+b=0
∴b=1;c=5
(2)当0≤x≤1时 x+1>0 ,x﹣1≤0,x-5![]() 0
0
则 |x+1|﹣|x﹣1|+2|x-5|
=x+1﹣(1﹣x)+2(5-x)
=x+1﹣1+x+10-2x
=10
(3)BC﹣AB的值不随![]() 的变化而改变,总为2
的变化而改变,总为2
![]() 秒时,点A表示的数为
秒时,点A表示的数为![]() ,点B表示的数为
,点B表示的数为![]() ,点C表示的数为
,点C表示的数为![]() ,
,
此时,BC=(![]() )-(
)-(![]() )=
)=![]() ,
,
AB=(![]() )-(
)-(![]() )=
)=![]() ,
,
所以BC-AB=( ∴BC﹣AB的值不随着时间t的变化而改变,总为2.![]() )-(
)-(![]() )=2
)=2


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】已知图甲是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
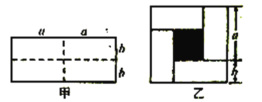
(1)求图乙中阴影部分正方形的边长(用含字母![]() ,
,![]() 的整式表示);
的整式表示);
(2)请用两种不同的方法求图乙中阴影部分的面积.
(3)观察图乙,并结合(2)中的结论,写出下列三个整式:![]() ,
,![]() ,
,![]() 之间的等量关系;
之间的等量关系;
(4)根据(3)题中的等量关系,解决如下问题:若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,AC=BC,∠ACB=45°,将三角形ABC沿着AC翻折,点B落在点E处,联结DE,那么![]() 的值为________.
的值为________.
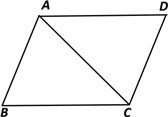
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A![]() 、A
、A![]() 、A
、A![]() …在射线ON上,点B
…在射线ON上,点B![]() 、B
、B![]() 、B
、B![]() …在射线OM上,△A
…在射线OM上,△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() …均为等边三角形,若OA
…均为等边三角形,若OA![]() =1,则△A
=1,则△A![]() B
B![]() A
A![]() 的边长为____
的边长为____
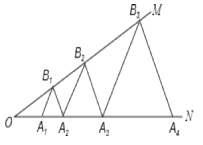
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面中,两条直线相交有一个交点,三条直线两两相交最多有3个交点,四条直线两两相交最多有6个交点……由此猜想,当相交直线的条数为n时,最多可有的交点数m与直线条数n之间的关系式为:m=_____.(用含n的代数式填空)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下图方式摆放餐桌和椅子,
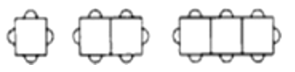 …
…
(1)1张长方形餐桌可坐4人,2张长方形餐桌拼在一起可坐______人.
(2)按照上图的方式继续排列餐桌,完成下表.
桌子张数 | 3 | 4 | 5 | n |
可坐人数 | ______ | ______ | ______ | ______ |
(3)一家餐厅有40张这样的长方形餐桌,某用餐单位要求餐厅按照上图方式,每8张长方形餐桌拼成1张大桌子,则该餐厅此时能容纳多少人用餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
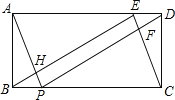
【题目】如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.
(1) 判断△BEC的形状,并说明理由;
(2) 求证:四边形EFPH是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片剪成四张大小一样的小正方形纸片,然后将其中一张正方形纸片再按同样方法剪成四张小正方形纸片,再将其中一张剪成四张小正方形纸片,如此进行下去.
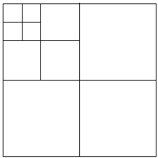
(1)填表:
剪的次数 | 1 | 2 | 3 | 4 | 5 |
纸片张数 | 4 | 7 |
(2)如果剪了100次,共剪出多少张纸片?
(3)如果剪了![]() 次,共剪出多少张纸片?
次,共剪出多少张纸片?
(4)能否剪若干次后共得到2019张纸片?若能,请直接写出相应剪的次数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=_____.

【答案】40°
【解析】试题分析:先根据三角形外角性质计算出∠EBF=∠A+∠E=85°,再根据圆内接四边形的性质计算出∠BCD=180°﹣∠A=125°,然后再根据三角形外角性质求∠F.
解:∵∠A=55°,∠E=30°,
∴∠EBF=∠A+∠E=85°,
∵∠A+∠BCD=180°,
∴∠BCD=180°﹣55°=125°,
∵∠BCD=∠F+∠CBF,
∴∠F=125°﹣85°=40°.
故答案为40°.
考点:圆内接四边形的性质;三角形内角和定理.
【题型】填空题
【结束】
17
【题目】某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一棵树,平均每棵树就会少结5个橘子.设果园增种x棵橘子树,果园橘子总个数为y个,则果园里增种 棵橘子树,橘子总个数最多.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com