
【题目】如图,已知:∠MON=30°,点A![]() 、A
、A![]() 、A
、A![]() …在射线ON上,点B
…在射线ON上,点B![]() 、B
、B![]() 、B
、B![]() …在射线OM上,△A
…在射线OM上,△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() …均为等边三角形,若OA
…均为等边三角形,若OA![]() =1,则△A
=1,则△A![]() B
B![]() A
A![]() 的边长为____
的边长为____
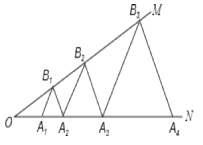
【答案】32
【解析】
根据等腰三角形的性质以及平行线的性质得出A![]() B
B![]() ∥A
∥A![]() B
B![]() ∥A
∥A![]() B
B![]() ,以及A
,以及A![]() B
B![]() =2B
=2B![]() A
A![]() ,得出A
,得出A![]() B
B![]() =4B
=4B![]() A
A![]() =4,A
=4,A![]() B
B![]() =8B
=8B![]() A
A![]() =8,A
=8,A![]() B
B![]() =16B
=16B![]() A
A![]() …进而得出答案.
…进而得出答案.
∵△A![]() B
B![]() A
A![]() 是等边三角形,
是等边三角形,
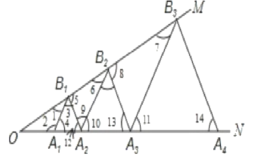
∴A![]() B
B![]() =A
=A![]() B
B![]() ,∠3=∠4=∠12=60°,
,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°120°30°=30°,
又∵∠3=60°,
∴∠5=180°60°30°=90°,
∵∠MON=∠1=30°,
∴OA![]() =A
=A![]() B
B![]() =1,
=1,
∴A![]() B
B![]() =1,
=1,
∵△A![]() B
B![]() A
A![]() 、△
、△![]() B
B![]() A
A![]() 是等边三角形,
是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A![]() B
B![]() ∥A
∥A![]() B
B![]() ∥A
∥A![]() B
B![]() ,
,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A![]() B
B![]() =2B
=2B![]() A
A![]() , A
, A![]() B
B![]() =4B
=4B![]() A
A![]() ,
,
∴A![]() B
B![]() =4B
=4B![]() A
A![]() =4,
=4,
A![]() B
B![]() =8B
=8B![]() A
A![]() =8,
=8,
A![]() B
B![]() =16B
=16B![]() A
A![]() =16,
=16,
以此类推:A![]() B
B![]() =32 B
=32 B![]() A
A![]() =32.
=32.
故答案为:32


科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣8,点C 在数轴上表示的数是10.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度也向右匀速运动.
![]()
(1)运动t秒后,点B表示的数是 ;点C表示的数是 .(用含有t的代数式表示)
(2)求运动多少秒后,BC=4(单位长度);
(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式![]() ,若存在,求线段PD的长;若不存在,请说明理由.
,若存在,求线段PD的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
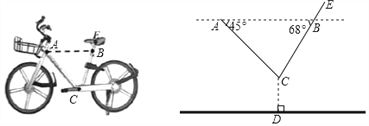
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
查看答案和解析>>
科目:初中数学 来源: 题型:
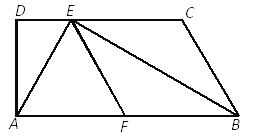
【题目】如图,已知梯形ABCD中,AB∥CD,∠D=90°,BE平分∠ABC,交CD于点E,F是AB的中点,联结AE、EF,且AE⊥BE.
求证:(1)四边形BCEF是菱形;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数大致图象是( )
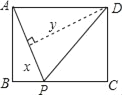
A. 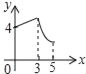 B.
B. 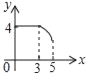 C.
C. 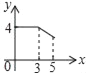 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若线段上的一个点把这条线段分成1:2的两条线段,则称这个点是这条线段的三等分点.如图1,点C在线段AB上,且AC:CB=1:2,则点C是线段AB的一个三等分点,显然,一条线段的三等分点有两个.
(1)已知:如图2,DE=15cm,点P是DE的三等分点,求DP的长.
(2)已知,线段AB=15cm,如图3,点P从点A出发以每秒1cm的速度在射线AB上向点B方向运动;点Q从点B出发,先向点A方向运动,当与点P重合后立马改变方向与点P同向而行且速度始终为每秒2cm,设运动时间为t秒.
①若点P点Q同时出发,且当点P与点Q重合时,求t的值.
②若点P点Q同时出发,且当点P是线段AQ的三等分点时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是最大的负整数,且
是最大的负整数,且![]() 、b、c满足(c﹣5)2+|
、b、c满足(c﹣5)2+|![]() +b|=0,请回答问题.
+b|=0,请回答问题.
![]()
(1)请直接写出![]() 、b、c的值:
、b、c的值:![]() = ,b= ,c= .
= ,b= ,c= .
(2)![]() 、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0 ≤ x ≤ 1时),请化简式子:|x+1|﹣|x﹣1|+2|x-5|(请写出化简过程).
、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0 ≤ x ≤ 1时),请化简式子:|x+1|﹣|x﹣1|+2|x-5|(请写出化简过程).
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和8个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,如图是小聪离家的距离![]() (单位:
(单位:![]() )与时间
)与时间![]() (单位:
(单位:![]() )的图象。根据图象回答下列问题:
)的图象。根据图象回答下列问题:
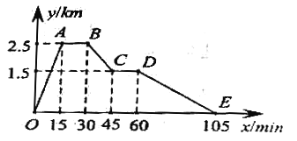
(1)体育场离小聪家______![]() ;
;
(2)小聪在体育场锻炼了______![]() ;
;
(3)小聪从体育场走到文具店的平均速度是______![]() ;
;
(4)小聪在返回时,何时离家的距离是![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象如图,则下列结论中正确的有( )
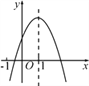
①a+b+c>0;②a-b+c<0;③b>0;④b=2a;⑤abc<0.
A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】试题解析:当x=1时,y=a+b+c,顶点坐标(1,a+b+c),
由图象可知,顶点坐标在第一象限,
∴a+b+c>0,故①正确;
当x=-1时,y=a-b+c,
由图象可知,当x=-1时,所对应的点在第四象限,
∴y=a-b+c<0,故②正确;
∵图象开口向下,
∴a<0,
∵x=-![]() =1,
=1,
∴b=-2a,故④错误;
∴b>0,故③正确;
∵图象与y轴的交点在y轴的上半轴,
∴c>0,
∴abc<0,故⑤正确;
∴正确的有4个.
故选B.
【题型】单选题
【结束】
10
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )

A. ![]() B. AD,AE将∠BAC三等分
B. AD,AE将∠BAC三等分
C. △ABE≌△ACD D. S△ADH=S△CEG
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com