
【题目】如图,∠1+∠2=180°,∠B=∠D.说明AB∥CD的理由.
补全下面的说理过程,并在括号内填上适当的理由
解:∵∠1+∠2=180°(已知)
∠2=∠AHB( )
∴ (等量代换)
∴DE∥BF( )
∴∠D=∠ ( )
∵∠ =∠B(等量代换)
∴AB∥CD( )

科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,M、E、F三点在 ![]() 上,N是矩形两对角线的交点.若
上,N是矩形两对角线的交点.若 ![]() =24,
=24, ![]() =32,
=32, ![]() =16,
=16, ![]() =8,
=8, ![]() =7,则下列哪一条直线是A、C两点的对称轴?( )
=7,则下列哪一条直线是A、C两点的对称轴?( ) 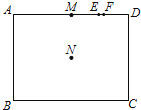
A.直线MN
B.直线EN
C.直线FN
D.直线DN
查看答案和解析>>
科目:初中数学 来源: 题型:
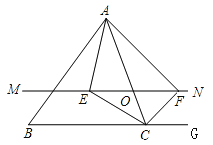
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2018的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=120°,∠COD=60°,OE平分∠BOC
(1)如图①.当∠COD在∠AOB的内部时
①若∠AOC=39°40′,求∠DOE的度数;
②若∠AOC=α,求∠DOE的度数(用含α的代数式表示),
(2)如图②,当∠COD在∠AOB的外部时,
①请直接写出∠AOC与∠DOE的度数之间的关系;
②在∠AOC内部有一条射线OF,满足∠AOC+2∠BOE=4∠AOF,写出∠AOF与∠DOE的度数之间的关系.
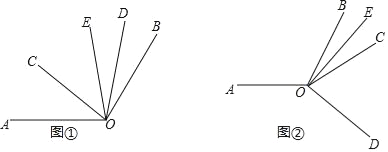
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
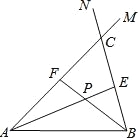
【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32![]() ,求AQ的长.
,求AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为24的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF= ![]() ,则小正方形的周长为( )
,则小正方形的周长为( ) 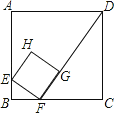
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com